Лекція 9. Багатомірні випадкові величини

На тому самому просторі елементарних наслідків можна розглядати не одну, а кілька випадкових величин. Наприклад, підкидають три гральних кубика. Можна розглядати одну випадкову величину ξ - суму очок, що випали, або три випадкових величини:

ξ₁ – число очок, що випали на 1-му кубику,

ξ₂ – число очок, що випали на 2-му кубику,

ξ ₃ – число очок, що випали на 3-му кубику.

В економіці, як правило, на показник діє кілька факторів, наприклад, якість продукції залежить від багатьох факторів.

Нехай ξ₁, ξ₂, …, ξ_n –система випадкових величин, визначених на множині .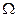

Функція розподілу системи випадкових величин визначається формулою

F(x₁, x₂, …, x_n) = P(ξ₁ <x₁, ξ₂ <x₂,....., ξ_n <x_n), (20)

де x₁, x₂, …, x_n ()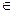

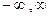При цьому F(x₁, x₂, …, x_n) – неспадна функція за кожним аргументом.

Для дискретної системи випадкової величини закон розподілу визначається задачім вектора x₁, x₂, …,x_n і вектора ймовірностей ,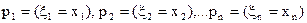

таких, що .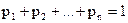

Функція розподілу виражається у вигляді кратної суми

F(x₁, x₂, …, x_n) = 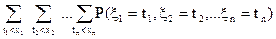, (21)

де підсумовування проводиться по всіх можливих значеннях кожної з випадкових величин, для яких .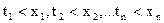

Система ξ₁, ξ₂, …, ξ_n називається неперервною, якщо існує f(x₁, x₂, …, x_n ) 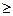0 така, що для будь-яких x₁, x₂, …, x_n функцію розподілу F(x) можна представити у вигляді n-мірного інтеграла

F(x) =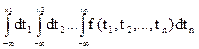. (22)

Функція f ( 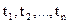) називається щільністю розподілу ймовірностей системи випадкових величин,

f(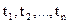) = 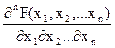(23)

в точках неперервності.

Випадкові величини ξ₁, ξ₂, …, ξ_n називаються незалежними, якщо для будь-яких

x₁, x₂, …, x_n незалежні події .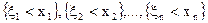

Для незалежних ξ₁, ξ₂, …, ξ_n функція розподілу дорівнює добутку функцій розподілу кожної випадкової величини

F(x₁, x₂, …, x_n) = 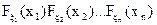(24)

Також справедливі рівності:

для дискретних випадкових величин р=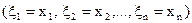

= ,

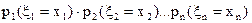для неперервних випадкових величин f() = .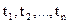

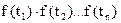Основними числовими характеристиками n випадкових величин є математичні сподівання

М(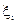) = 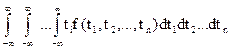(25)

і дисперсії

D(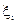) = = 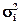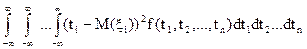. (26)

Умовним законом розподілу однієї випадкової величини, що входить у систему, називається закон, знайдений за умови, що інша випадкова величина, що входить у цю же систему, прийняла певне значення. Умовний закон розподілу задається як функцією розподілу, так і щільністю розподілу. Якщо розглядається розподіл випадкової величини ξ_i за умови, що інша випадкова величина ξ_j прийняла певне значення, то умовна функція розподілу позначається F(x/y), а щільність - f(x/ y). Важливими характеристиками є умовні математичні сподівання й умовні дисперсії. Нехай випадкова величина ξ_i приймає значення

a = (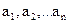), а випадкова величина ξ_j - b = ().

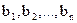Умовним математичним сподіванням дискретної випадкової величини ξ_i при ξ_j = b називають суму добутків можливих значень ξ _i на їхні умовні ймовірності_. Тоді умовне математичне сподівання обчислюється за формулою:

M(ξ_i / ξ_j =b) = 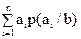. (27)

Для неперервних випадкових величин

M(ξ_i / ξ_j =b) = 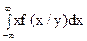. (28)

Особлива роль у вивченні системи випадкових величин належить кореляційному моменту

(коваріації). Коваріацією випадкових величин ξ _i і ξ_j називається число

= cov(ξ_iξ_j) = M((ξ _i-M(ξ _i))(ξ _j-M(ξ_j)))=M(ξ_iξ_j)-M(ξ_i)M(ξ_j), i,j=1,2,…n (29)

Для незалежних випадкових величин коваріація дорівнює нулю, тому що в цьому випадку M(ξ_iξ_j) = M(ξ_i)M(ξ_j).

Очевидно, що 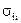= =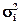 D(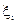), cov(ξ_iξ _j) = cov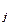(ξξ)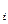

Всі парні коваріації становлять симетричну щодо головної діагоналі коваріаційну матрицю розмірністю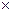 (nn).

=

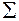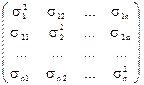
Визначник коваріаційної матриці є узагальненою дисперсією системи випадкових величин.

Розглянемо систему тільки двох випадкових величин, нехай ξ₁, ξ_2. Нехай випадкова величина ξ₁ приймає значення з множинаі X, ξ₂ – з множинаі Y, (X,Y) - дійсні числа. Мірою лінійної залежності двох випадкових величин ξ₁, ξ₂ є коефіцієнт кореляції

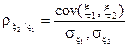, (30)

Властивості коефіцієнта кореляції:

1. |ρ|.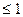

2. |ρ|=1 тоді й тільки тоді, коли між випадковими величинами існує

лінійний функціональний взаємозв'язок

y = аx + b, (31)

де ,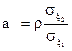

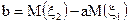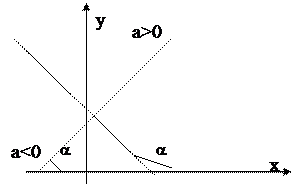
причому, якщо ρ = 1, то a > 0, якщо ρ = -1, то a < 0 (Рисунок 15)

Для незалежних випадкових величин ρ = 0, але обернене твердження невірне, тому що між випадковими величинами може бути інший тип взаємозв'язку (нелінійний). Чим ближче значення ρ до нуля, тим слабкіше лінійний взаємозв'язок, чим ближче по модулю до одиниці, тим - сильніше. Якщо ρ = 0, то говорять, що випадкові величини некорельовані. Можна показати, що якщо нормально розподілені випадкові величини некорельовані, то вони незалежні.

Рисунок 15. Лінійний функціональний взаємозв'язок

.

Нехай –1<ρ<1 і ρ≠0. Якщо нанести точки (X,Y) на координатну площину Xo, то можна помітити, що ці точки групуються навколо деякої прямої y = ax + b. Обчислимо коефіцієнти a,b ції прямої за умови, що дисперсія 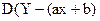відхилень точок (X,Y) від точок на прямій була мінімальна.

.

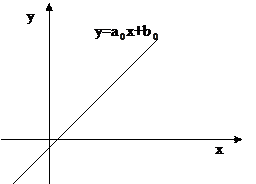Дата добавления: 2014-01-07