Числові характеристики вибіркового розподілу

Лекція 13.

Нехай 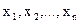- вибірка обсягу n з генеральної сукупності з функцією розподілу F(x). Розглянемо вибірковий розподіл, тобто розподіл дискретної випадкової величини, що приймає значення 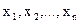з ймовірностями, рівними 1/n. Числові характеристики цього вибіркового розподілу називаються вибірковими (емпіричними) характеристиками.

Слід зазначити,що вибіркові числові характеристики є характеристиками даної вибірки, але не є характеристиками розподілу генеральної сукупності. Щоб підкреслити це розходження, вибіркові характеристики надалі будемо позначати зі значком * нагорі. Тоді, використовуючи формули параграфа «Числові характеристики випадкових величин», одержимо

m* = , (45)

D* = 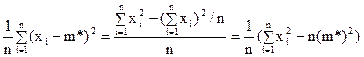. (46)

Для статистичних рядів формули (1) і (2) перетворяться відповідно

m* =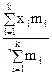, , 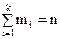(47)

D* = 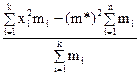. (48)

Обчислимо m* і D* для статистичного ряду, наведеного в Прикладі 20.

Всі обчислення зведемо в Таблицю 6.

Таблиця 6. Допоміжні обчислення

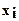
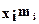
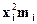
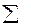
Отримані дані підставимо у формули (47) і (48), одержимо

m* = 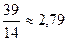, D* =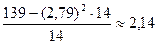

Вибірковою модою Md* унімодального (одновершинного) розподілу називається елемент вибірки, що зустрічається з найбільшою частотою.

Вибірковою медіаною називається число Mn*, що ділить варіаційний ряд на дві частини, що містять рівне число елементів.

Вибіркові коефіцієнти асиметрії й ексцесу обчислюються за формулами

А* = 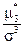, (49)

Е* = 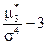. (50)

Вибіркові числові характеристики двовимірної вибірки обчислюються як відповідні числові характеристики двовимірного випадкового вектора (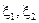) дискретного типу, з огляду на те що значення (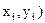, i=1,2,…,n, вектор приймає з ймовірностями, рівними 1/n. Вибіркові середні 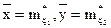й дисперсії 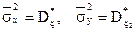знаходяться за формулами (45) і (46), а вибірковий коефіцієнт кореляції за формулою

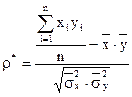(51)

Приклад 22. Обчислити вибіркові середні, дисперсії й коефіцієнт кореляції для вибірки, наведеної в Таблиці 7.

Таблиця 7. Двовимірного вибірка

x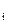
y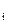

Обчислення зручно виконувати в наступній послідовності:

,

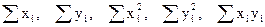потім обчислит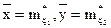и й 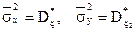і, нарешті 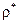. Обчислення звичайно зводяться в Таблицю 8.

Таблиця 8. Допоміжні обчислення

15

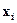
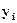
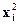
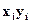
Підставляючи знайдені суми у формули (1) і (2) одержимо:

.

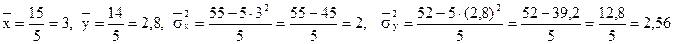
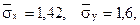
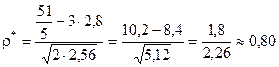Вибіркова лінійна регресія 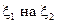визначається рівнянням

.

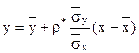Для нашого приклада .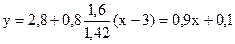

Аналогічно визначається вибіркова лінійна регресія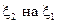

.

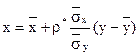Для нашого приклада

.

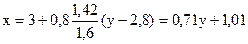Поле точок і прямі регресії зображені на Рисунку 19.

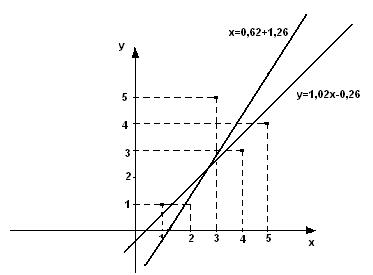
Рисунок 19. Поле точок і прямі регресії

Лекція 14. Методи оцінювання параметрів

Дата добавления: 2014-01-07