
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перевірка гіпотези про вид розподілу генеральної сукупності
|
|
|
|
Критерій і його застосування
Розглянуті вище гіпотези відносились до окремих параметрів розподілу випадкової величини, причому закон її розподілу вважався відомим. Однак у багатьох практичних задачах точний закон розподілу досліджуваної випадкової величини невідомий тобто є гіпотезою, що вимагає статистичної перевірки.
Нехай 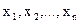 - вибірка спостережень випадкової величини
- вибірка спостережень випадкової величини 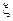 . Перевіряється гіпотеза
. Перевіряється гіпотеза 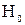 , яка стверджує, що
, яка стверджує, що 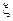 має функцію щільності розподілу f(x,
має функцію щільності розподілу f(x,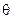 ).
).
Перевірка гіпотези 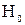 за допомогою критерію
за допомогою критерію 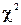 здійснюється за наступною схемою. За вибіркою спостережень знаходять оцінки невідомих параметрів
здійснюється за наступною схемою. За вибіркою спостережень знаходять оцінки невідомих параметрів 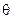 передбачуваного закону розподілу випадкової величини
передбачуваного закону розподілу випадкової величини  . Далі область можливих значень випадкової величини розбивається на k множин
. Далі область можливих значень випадкової величини розбивається на k множин 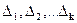 . Наприклад, на k інтервалів у випадку, коли
. Наприклад, на k інтервалів у випадку, коли  - неперервна випадкова величина, або k груп, що складаються з окремих значень, для дискретної випадкової величини
- неперервна випадкова величина, або k груп, що складаються з окремих значень, для дискретної випадкової величини  . Нехай
. Нехай 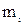 - число елементів вибірки, що належить множині
- число елементів вибірки, що належить множині 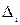 , i = 1,2,…,n.Очевидно, що
, i = 1,2,…,n.Очевидно, що 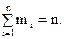 Використовуючи передбачуваний закон розподілу випадкової величини
Використовуючи передбачуваний закон розподілу випадкової величини  , знаходять ймовірність
, знаходять ймовірність 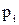 того, що значення
того, що значення  належить множині
належить множині 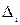 , тобто
, тобто 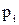 = P(
= P( ), i = 1,2,…,k... Очевидно. що
), i = 1,2,…,k... Очевидно. що 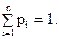 Вибіркове значення статистики
Вибіркове значення статистики 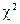 обчислюється за формулою
обчислюється за формулою
 . (66)
. (66)
Гіпотеза 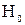 погоджується з результатами спостережень на рівні значущості
погоджується з результатами спостережень на рівні значущості 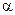 , якщо
, якщо
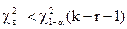 ,
,
де 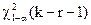 - квантиль порядку
- квантиль порядку  розподілу
розподілу 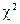 з k – r -1порядками волі, k- число інтервалів, а r – число невідомих параметрів розподілу, що оцінюються за вибіркою. Якщо ж
з k – r -1порядками волі, k- число інтервалів, а r – число невідомих параметрів розподілу, що оцінюються за вибіркою. Якщо ж 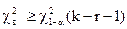 , то гіпотеза
, то гіпотеза 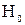 відхиляється.
відхиляється.
Зауваження. Призастосуванні критерію 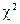 необхідно, щоб для всіх інтервалів виконувалася умова
необхідно, щоб для всіх інтервалів виконувалася умова 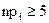 . Якщо в деяких інтервалах ця умова не виконується, то їх варто об'єднати із сусідніми.
. Якщо в деяких інтервалах ця умова не виконується, то їх варто об'єднати із сусідніми.
Приклад 27. Перевіримо на рівні значущості 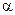 = 0,1 гіпотезу про нормальний розподіл вибірки із Приклада 20.
= 0,1 гіпотезу про нормальний розподіл вибірки із Приклада 20.
Обчислимо спочатку оцінку математичного сподівання 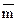 й оцінку дисперсії
й оцінку дисперсії 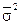 , для цього складемо Таблицю 11.
, для цього складемо Таблицю 11.
Таблиця 11. Допоміжні обчислення, для оцінки математичного сподівання 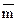 й оцінки дисперсії
й оцінки дисперсії 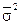
| Номер інтервалу i | Границі інтервалу | Середина
інтервалу
x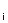
| Частота
m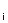
| x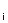 m m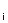
| x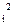 m m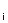
|
| 14 - 23 | 18,5 | 37,0 | 684,50 | ||
| 23 - 32 | 27.5 | 82,5 | 2268,75 | ||
| 32 -41 | 31,5 | 219,0 | 7993,50 | ||
| 41 -50 | 45,5 | 773,5 | 35194,25 | ||
| 50 -59 | 54,5 | 545,0 | 29702,50 | ||
| 59 -68 | 63,5 | 571,5 | 36290,25 | ||
| 68 -77 | 72,5 | 217,5 | 15768,75 | ||
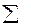
| - | - | 2453,0 | 127902,50 |
n = 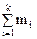 = 50, k = 7,
= 50, k = 7, 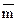 =
= 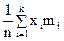 =
=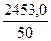 = 49,06
= 49,06
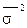 =
=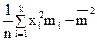 =
= 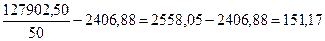
 =
= 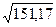 = 12,30
= 12,30
Ймовірності 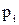 = P(
= P( ) обчислимо за формулою
) обчислимо за формулою
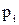 = P(
= P( )=
)= 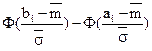 , i=1,2,..,7,
, i=1,2,..,7,
де 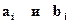 - відповідно нижня й верхня границі інтервалів, а значення
- відповідно нижня й верхня границі інтервалів, а значення 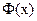 беруться з таблиці Додатка 2.
беруться з таблиці Додатка 2.
Складемо нову Таблицю 12, розширивши перший і останній інтервали.
Таблиця 12. Обчислення ймовірностей 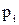 = P(
= P( )
)
| Номер інтер- валу i | Границі інтервалу | Частота
m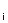
| 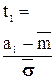
| 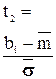
| 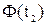
| 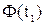
| 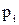
|
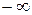 - 23 - 23
| 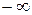
| -2,12 | 0,0170 | 0,0170 | |||
| 23 - 32 | -2,12 | -1,39 | 0,017 | 0,0823 | 0,0653 | ||
| 32 -41 | -1,39 | -0,66 | 0,0823 | 0,2546 | 0,1723 | ||
| 41 -50 | -0,66 | 0,08 | 0,2546 | 0,5319 | 0,2773 | ||
| 50 -59 | 0,08 | 0,81 | 0,5319 | 0,7910 | 0,2591 | ||
| 59 -68 | 0,81 | 1,54 | 0,7910 | 0,9382 | 0,1472 | ||
68 -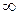
| 1,54 | 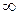
| 0,9382 | 0,0618 |
Для обчислення 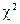 за формулою (20) складемо ще одну таблицю, об’єднуючи при цьому перший інтервал із другим і сьомий інтервалом із шостим.
за формулою (20) складемо ще одну таблицю, об’єднуючи при цьому перший інтервал із другим і сьомий інтервалом із шостим.
Таблиця 13.Обчислення 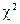
| Номер інтер- валу i | 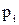
| n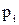
| 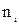
| 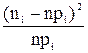
|
 0,0823
0,0823
|
4,115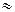 4 4
| 0,25 | ||
| 0,1723 | 8,615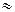 9 9
| 1,00 | ||
| 0,2773 | 13,865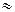 14 14
| 0,64 | ||
| 0,2591 | 12,955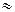 13 13
| 0,69 | ||
| 0,2090 |
10,450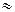 10 10
| 0,40 | ||
| Сума | 2,98 |
Сума чисел остатнього стовпця є вибіркове значення критерію, 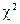 = 2,98. За таблицею квантилей розподілу
= 2,98. За таблицею квантилей розподілу 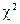 знайдемо
знайдемо 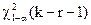 . Після об'єднання, число інтервалів k=5, число параметрів нормального розподілу r=2,
. Після об'єднання, число інтервалів k=5, число параметрів нормального розподілу r=2, 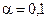 . Тоді
. Тоді 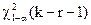 =
=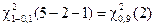 = 4,61. Вибіркове значення статистики критерію дорівнює 2,98 і це значення менше, ніж
= 4,61. Вибіркове значення статистики критерію дорівнює 2,98 і це значення менше, ніж 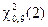 =0,64, отже гіпотеза про нормальний розподіл вибірки приймається.
=0,64, отже гіпотеза про нормальний розподіл вибірки приймається.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 513; Нарушение авторских прав?; Мы поможем в написании вашей работы!