
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доведення. Розглянемо два послідовні наближення
|
|
|
|
Розглянемо два послідовні наближення  .
.  . Тоді
. Тоді  . Будемо надавати числу n заначень: 1, 2, 3,...
. Будемо надавати числу n заначень: 1, 2, 3,...
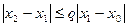

...
 (6)
(6)
Розглянемо ряд  , бачимо, що
, бачимо, що  . З нерівності (6) слідує, що ряд збіжний, тоді
. З нерівності (6) слідує, що ряд збіжний, тоді 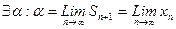 перейшовши до границі в (3) отримаємо, що
перейшовши до границі в (3) отримаємо, що 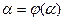 - розв’язок рівняння (2).
- розв’язок рівняння (2).
Доведемо єдиність. Нехай  тоді
тоді 
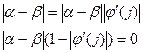
остання дужка завжди не дорівнює нулю. . Корінь єдиний. Візьмемо будь-яке число
. Корінь єдиний. Візьмемо будь-яке число  і
і
 перейти до границі при
перейти до границі при  отримаємо нерівність (5).
отримаємо нерівність (5).
Для доведення (1) до виду (2) можна застосувати такий метод. Замінимо рівняння (1) рівносильним рівнянням 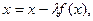 де
де 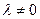 , та
, та  повинно таке, що
повинно таке, що  , тобто
, тобто 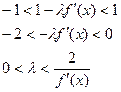 , тобто якщо знак функції
, тобто якщо знак функції 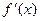 на [a,b] не змінився, то
на [a,b] не змінився, то повинна мати той самий знак, що й
повинна мати той самий знак, що й 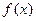 і задовольняти нерівність
і задовольняти нерівність 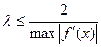 (7)
(7)
Н-д: перетворити рівність  , до виду
, до виду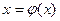 , так щоб
, так щоб 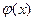 задовольняла всі умови теореми, якщо розв’язок
задовольняла всі умови теореми, якщо розв’язок 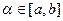
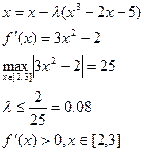
візьмемо  =0.079, тоді отримаємо
=0.079, тоді отримаємо
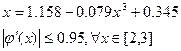
вхідні дані 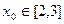 оцінка точності.
оцінка точності.
Зауваження: для оцінки точності на практиці зручно користуватись формою: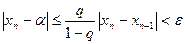 ,
,  (8)
(8)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 340; Нарушение авторских прав?; Мы поможем в написании вашей работы!