Диференціювання функцій інтерпольованих многочленами Лагранжа

Залишимо в силі умови попереднього параграфа. Замінимо функцію 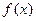інтерполяційним многочленом: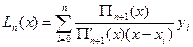

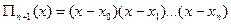, поділимо кожну дужку на 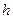і домножимо на .

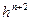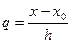
тоді ,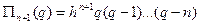

,

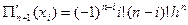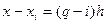підставимо .

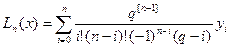Тоді 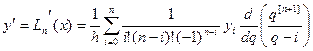. Похибка у випадку многочлена Лагранжа рівна: ,

.

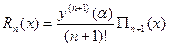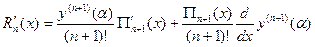У випадку, коли 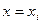, тоді .

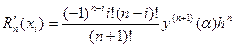Зауваження: часто похибка, яка виникає при обчисленні похідних може набагато перевищувати похибку задання самої функції(навіть може зростати до ).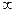

Наприклад: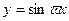

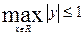
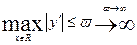
§11 ЗАДАЧА ЧИСЕЛЬНОГО ІНТЕГРУВАННЯ ФУНКЦІЇ. ФОРМУЛИ ПРЯМОКУТНИКІВ

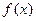
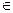
Якщо функція 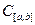, то 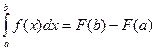, але часто первісна 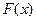не може бути знайдена за допомогою таблиці інтегралів (інтеграл не обчислюється) або є складним аналітичним виразом. Крім того на практиці часто підінтегральна функція задана у вигляді таблиці, в усіх цих випадках застосовують чисельне інтегрування, тобто задача чисельного інтегрування полягає в знаходженні значень визначеного інтеграла на основі ряду значень підінтегральної функції. Якщо мова йде про одномірний інтеграл, то відповідні формули чисельного інтегрування називаються квадратурними.

Однією з найпростіших квадратурних формул є формула прямокутників.

f(x) - беруть точку

a b

площу трапеції замінюють площею прямокутника

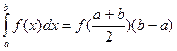(1)- формула середніх прямокутників.

При цьому похибка .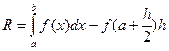

Тоді можна записати 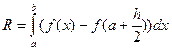.(2)

Використаємо розклад в ряд Тейлора функції f(x) в точці :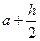

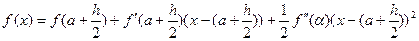,(3) 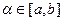. Підставимо (3) в(2):

,

, .

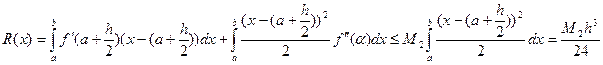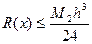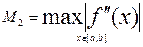Розбивши 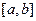на частини точками , де 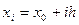, , 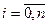, 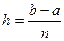застосувавши формулу (1) на кожному з цих відрізків отримаємо:

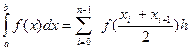- узагальнена формула прямокутників.

Похибка останньої формули буде дорівнювати сумі похибок на кожному з відрізків .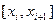

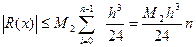
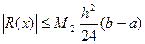
Дата добавления: 2014-01-07