
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
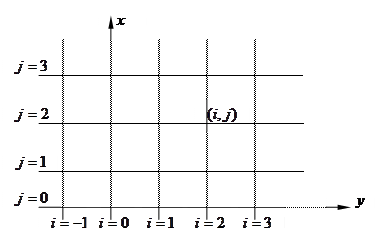
Метод сіток розв’язування лінійних диференціальних рівнянь гіперболічного типу
|
|
|
|
Розглянемо метод сіток для розв’язування диференціальних рівнянь такого типу:
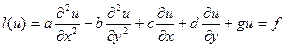 (1)
(1)
де 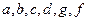 - функції змінних х та у.
- функції змінних х та у.
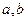 - одного знаку
- одного знаку
Задача1: під нею розуміють розв‘язок задачі Коші яка полягає в відшуканні розв‘язку задачі (1) в області 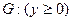 , який задовольняє:
, який задовольняє:
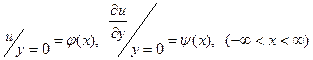 (2)
(2)
Задача2: Розв‘язок змішаної задачі яка полягає в відшуканні розв‘язку рівняння (1) в області:
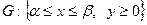 ,
,
який задовольняє початкові умови:
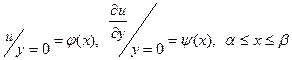 (3)
(3)
і деякі умови на прямих:
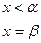
Розглядають три типи умов на прямих, що обмежують область:
1) 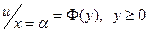 (4)
(4)
2) 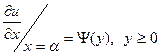 (5)
(5)
3) 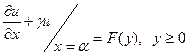 (6)
(6)
Аналогічно так само на прямій 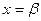
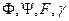 - задані функції.
- задані функції.
Розглянемо метод сіток:

Для кожного внутрішнього вузла диференціального рівняння (1) замінимо різницевим рівнянням замінивши відповідні похідні наступним способом:
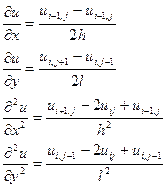
Підставимо цю заміну в рівняння (1) маємо:
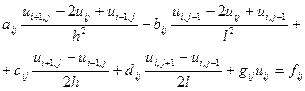 (7)
(7)
або:
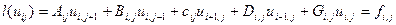 (8)
(8)
де: 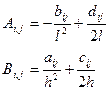
З останнього рівняння (8) видно, що знаючи значення розв‘язку в вузлах 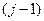 і
і 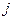 рядка в усіх вузлах
рядка в усіх вузлах 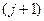 рядка. Тому для розв‘язку задачі необхідно знати значення в усіх вузлах рядків
рядка. Тому для розв‘язку задачі необхідно знати значення в усіх вузлах рядків 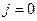 і
і 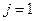 .
.
Ці значення шукають з початкових умов з одним з наступних способів:
1) Початкові умови:
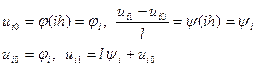 (8‘)
(8‘)
2) Введемо додатковий (-1) рядок. Значення 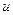 на цьому рядку нас не цікавлять. Але початкові умови:
на цьому рядку нас не цікавлять. Але початкові умови:
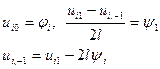
Підставивши (8) 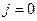 маємо:
маємо:
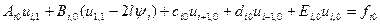
Таким чином значення розв‘язку на перших двох рядках будуть знайдені за формулою:
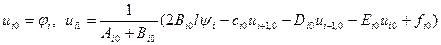 (9)
(9)
Значення розв‘язку на рядках шукають за (9) або (8‘).
Зауваження: У випадку рівняння
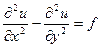 (10)
(10)
і квадратичної сітки 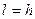 , різницеве рівняння набуде вигляду:
, різницеве рівняння набуде вигляду:
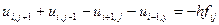 (11)
(11)
Для обчислення значення на перших двох рядках отримаємо наступне:
1) 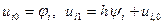
2) 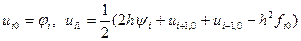
Будемо вважати, що у розв‘язку 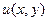 існує до четвертого порядку.
існує до четвертого порядку.
Використавши розклад в ряд Тейлора аналогічно до еліптичних рівнянь отримаємо:
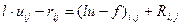
де: 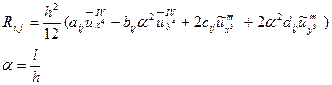
Позначивши 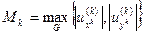
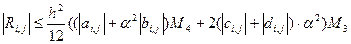 (12)
(12)
Похибки апроксимації початкових умов.
У випадку формул (8‘) перша умова похибки не дає, а друга умова дає похибку:
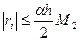
У випадку (9) похибка буде:
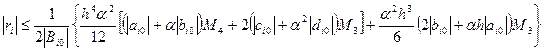
Означення: Різницева схема називається Явною якщо для довільного J кожне з рівнянь яке пов‘язує значення шуканого розв‘язку на горизонтальних рядах 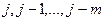 входить лише одна точка ряду
входить лише одна точка ряду 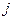 так, що значення розв‘язку в кожній точці
так, що значення розв‘язку в кожній точці 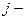 го рядку можна знайти незалежно від його значень в інших точках цього рядка.
го рядку можна знайти незалежно від його значень в інших точках цього рядка.
Означення: Різницева схема називається неявною, якщо для відшукання значень на 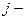 му рядку при умові, що значення на попередніх рядках відомі необхідно розв‘язати систему рівнянь яка пов‘язує значення розв‘язку в кількох точках
му рядку при умові, що значення на попередніх рядках відомі необхідно розв‘язати систему рівнянь яка пов‘язує значення розв‘язку в кількох точках 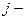 го рядка.
го рядка.
Наведена вище схема є явною.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 723; Нарушение авторских прав?; Мы поможем в написании вашей работы!