Метод сіток розв‘язування лінійних диференціальних рівнянь параболічного типу

Поняття стійкості різницевих схем.

Нехай задано диференціальне рівняння:

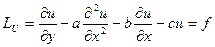(1)

де - задані функції змінних .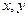

п.1. Метод сіток для розв‘язування задачі Коші.

Нехай нам потрібно знайти 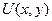рівняння (1). У півплощині 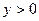який задовольняє:

(2)

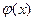- задана.

Розглянемо дві сім‘ї паралельних прямих.

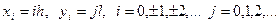
Для довільного вузла , 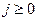похідні з рівняння (1) замінимо:

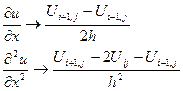
Похідну по 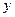в вузлі будемо замінювати одним з трьох способів.

(*)

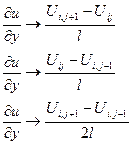В залежності від цього отримаємо три типи різні апроксимації рівняння (1):

(3)

Аналогічно використовуючи два останніх рівняння (*) отримаємо відповідно апроксимації (4) і (5)

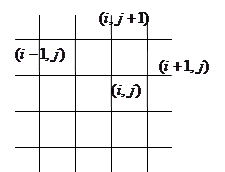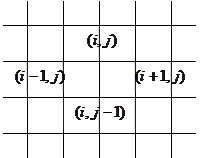1) 2)

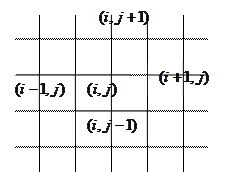3)

Перша і третя схеми явні, друга – неявна.

Для вузлів нульового горизонтального ряду з умови (2) маємо:

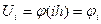
Якщо диференціальне рівняння (1) записати у вигляді:

(6),

то рівняння (3)-(5) спрощуються (будемо позначати, що)

1) 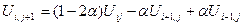(7)

2) (8)

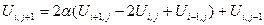3) (9)

Число 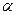підбирають як омога простіші.

п.2. Метод сіток для розв‘язування мішаних задач.

(10)

Задачу будемо формулювати так: Знайти розв‘язок рівняння (10) в прямокутнику (11). Який задовольняє початкові умови (2):

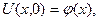(12) і

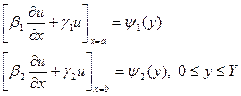(13)

де: 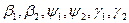- задані функції змінної .

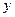Розглянемо сітку точок:

де: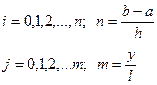

Вузли яких лежать на прямих 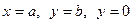будемо вважати граничними, всі інші внутрішні.

Для внутрішніх вузлів будемо мати рівняння (7)-(9).

Для вузлів які лежать на прямій маємо:

Для граничних вузлів на прямих запишемо:

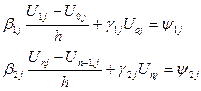(14)

Тому знову отримаємо три різницеві схеми. Перша це рівняння (7) для

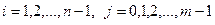і умови (14).

Друга схема це рівняння (8) і (14). Третя це рівняння (9) і (14).

До всіх трьох схем також додається рівність:

п.3. Поняття стійкості різницевих схем.

При проведенні обчислень за деякою схемою неминучим є заокруглення результатів.

Бувають випадки коли похибка заокруглень (або помилка), яка виникла на певному кроці зростає дуже швидко і врешті спотворює результат.

Наприклад: Розглянемо схему:

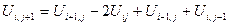
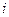
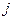
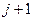
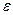
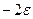
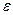
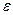
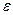
Означення: Різницеву схему називають стійкою, якщо обчислювальна похибка при переході від одного ряду до іншого не зростає. В протилежному випадку вона є нестійкою.

Дата добавления: 2014-01-07