Задачі до розділу 3.1

Задача 3.1.1

Від складських приміщень до цеху постачання здійснюються двома вантажними автомобілями. Ймовірність того, що кожна вантажівка вчасно прибуде до цеху дорівнює 0.95. Знайти ймовірність того, що хоча б одна з вантажівок прибуде вчасно.

Рішення

Подія А – хоча б одна з вантажівок прибуде вчасно. Подія А складається з появи хоча б однієї з подій: 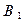- вчасне прибуття 1-ї вантажівки; 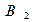- вчасне прибуття 2-ї вантажівки, що є незалежними подіями, тоді:

,

,

,

.

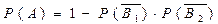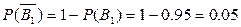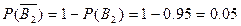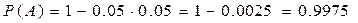Задача 3.1.2

Пристрій складається з трьох незалежно працюючих елементів. Ймовірність відмови елементів відповідно дорівнюють – 0,06; 0,05 і 0,08. Знайти ймовірність відмови пристрою, якщо для цього достатньо, щоб відмовив хоча б один елемент.

Рішення

Подія А складається з появи хоча б однієї з подій:

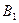- відмовив I елемент;

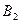- відмовив II елемент;

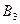- відмовив III елемент, що є незалежними подіями, тому:

,

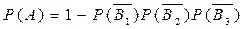де

;

;

;

.

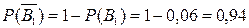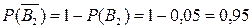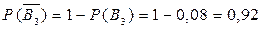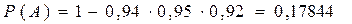Задача 3.1.3

Троє стрільців зробили постріл по цілі. Ймовірність влучення в ціль першого стрільця 0,75, другого – 0,65 і третього – 0,9. Знайти ймовірність того, що хоча б один зі стрільців влучить у ціль.

Задача 3.1.4

Студент розшукує потрібну формулу в двох довідниках. Ймовірність того, що формула міститься в першому довіднику 0,7, в другому довіднику – 0,65. Знайти ймовірність того, що формула міститься хоча б в одному з довідників.

Розділ 3.2. Формула повної ймовірності

Теорема: Ймовірність події А, яка може відбутися лише при умові появи однієї з несумісних подій В₁, В₂, …, В_п , які утворюють повну групу, дорівнює сумі добутків ймовірностей кожної з цих подій на відповідну умовну ймовірність події А.

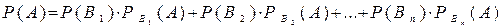. (3.3)

Доведення

Подія А може відбутися, якщо відбудеться одна з несумісних подій В₁, В₂, …, В_п . Тобто поява події А означає здійснення однієї, будь якої з несумісних подій , , 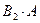…, 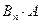Використовуючи теорему додавання (формула 2.1), одержимо

.

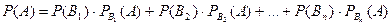Оскільки подія А і події В₁, В₂, …, В_п залежні, тоді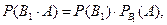

……………………..

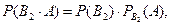
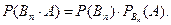
Звідки .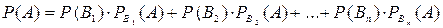

Наприклад:

У першій коробці міститься 15 приладів, з яких 14 якісних, а у другій – 20 приладів, з яких – 17 якісних. Із першої коробки навмання вилучають прилад і перекладають його у другу коробку. Знайти ймовірність того, що прилад, який вилучили з другої коробки, є якісним.

Рішення

Подія А – з другої коробки вилучили якісний прилад.

Тоді мають місце гіпотези (припущення) щодо того, який прилад вилучили з першої коробки:

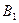- з першої коробки вилучили якісний прилад;

- з першої коробки вилучили неякісний прилад.

Тоді: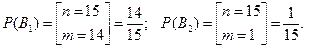

Знайдемо умовні ймовірності того, що з другої коробки вилучили якісний прилад, якщо з першої коробки вилучили якісний прилад 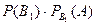та якщо з першої коробки вилучили неякісний прилад :

;

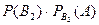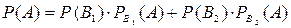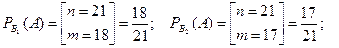
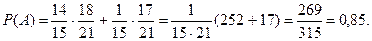
Дата добавления: 2014-01-07