Задачі до розділу 3.2

Задача 3.2.1

На базі зберігається однотипна продукція трьох підприємств, причому 30% - продукція I підприємства, 50% - продукція II підприємства, 20% - продукція III підприємства. Якісна продукція I підприємства складає 95%, II підприємства – 80%, III підприємства -70%. Знайти ймовірність того, що навмання обрана одиниця продукції буде якісною.

Рішення

Подія А - навмання обрана одиниця продукції буде якісною.

Можливі наступні гіпотези:

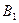- обрана продукція належить I підприємству;

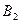- обрана продукція належить II підприємству;

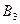- обрана продукція належить III підприємству.

За умовою задачі, ймовірності цих гіпотез наступні:

;

;

.

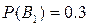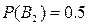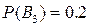Умовна ймовірність того, що одиниця продукції якісна, якщо вона виготовлена на I підприємстві буде

.

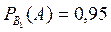Умовна ймовірність того, що одиниця продукції якісна, якщо вона виготовлена на II підприємстві буде

.

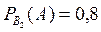Умовна ймовірність того, що одиниця продукції якісна, якщо вона виготовлена на III підприємстві буде

.

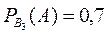Ймовірність того, що навмання обрана одиниця продукції буде якісною, визначається за формулою повної ймовірності

,

.

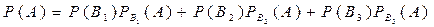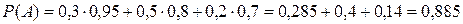Задача 3.2.2

У інформаційному центрі є комп’ютери двох фірм-виробників. Ймовірність того, що під час виконання розрахунків за деякою програмою комп’ютер першої фірми-виробника вийде з ладу 0,05, другої 0,2. Науковець робить розрахунки на навмання обраному комп’ютері. Знайти ймовірність того, що до кінця виконання розрахунків комп’ютер не вийде з ладу.

Задача 3.2.3

У першій урні знаходиться 10 кульок, з яких 8 білих, у другій урні – 20 кульок, з яких 4 білі. З кожної урни навмання вилучили по одній кульці а потім з цих двох кульок навмання обрано одну. Знайти ймовірність того, що обрано білу кульку.

Розділ 3.3. Ймовірність гіпотез. Формули Бейєса

Нехай проведено випробування за результатами якого з’явилася подія А. Знайдемо умовні ймовірності 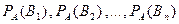(ймовірність того, що подія 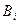відбудеться, якщо подія А вже відбулася). Наприклад, для події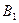

,

,

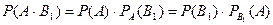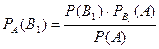де 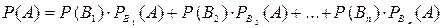- повна ймовірність.

У загальному вигляді

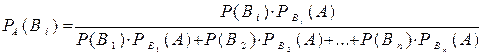, (3.4)

де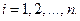

Одержану формулу (3.4) називають формулою Бейєса (за ім’ям англійського математика, який вивів цю формулу і опублікував у 1764 році). Формула Бейєса дозволяє переоцінити ймовірність гіпотез після того, як стане відомим результат випробування, тобто з’явиться подія А.

Наприклад: Деталі, що виготовляє цех заводу попадають на перевірку на стандартність до одного з двох контролерів. Ймовірність того, що деталь попаде до першого контролера, дорівнює 0,55, а до другого – 0,45. Ймовірність того, що деталь буде названо стандартною першим контролером – 0,95, а другим – 0,98. Деталь при перевірці було названо стандартною. Знайти ймовірність того, що цю деталь перевірив перший контролер.

Дата добавления: 2014-01-07