Вибір як максимізація критерію

Якщо тепер зробити ще одне важливе припущення, що вибір довільної альтернативи приводить до однозначно відомим наслідкам (тобто вважати, що вибір здійснюється в умовах визначеності) та заданий критерій q (x) чисельно виражає оцінку цих наслідків, то найкращою альтернативою x ^* є, істотно, та, що має найбільше значення критерію:

x ^*. = arg 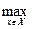(x). (1)

Задача пошуку x ^*, що є простою за постановкою, часто виявляється складною для розв’язку, оскільки метод її розв’язку (та й сама його можливість) визначається як характером множини X (розмірністю вектора x та типом множини X - чи є вона скінчена, зчисленна або континуальна), так і характером критерію (чи являється q (x ) функцією або функціоналом та якою, чи яким саме?).

Однак, складність пошуку найкращої альтернативи суттєво зростає, тому що на практиці оцінювання довільного варіанта одним числом звичайно є неприпустимим спрощенням. Більш повний розгляд альтернатив приводить до необхідності оцінювати їх по декільком критеріям, що якісно різняться між собою. Наприклад, при виборі конструкції літака враховують множину критеріїв: технічних (висотність, швидкість, маневреність, вантажопідйомність, тривалість польоту тощо), технологічних (зв’язаних з майбутнім процесом серійного виробництва літаків), економічних (визначаючих витрати на виробництво, експлуатацію та обслуговування машин, їх конкурентноздатність), ергономічних (умови роботи екіпажу, рівень комфорту для пасажирів) й інше.

Отже, нехай для оцінювання альтернатив використовуються декілька критеріїв q_i (x ), i = . Теоретично можна уявити собі випадок, коли множині X належить одна альтернатива, що володіє найбільшим значенням усіх p критеріїв. Вона і є найкращою. Однак, на практиці такі випадки майже не зустрічаються, і виникає питання, як же тоді виконати вибір.

q₁ q₂

q_{0 1} x₁^* x₂^*

∆q₂

x₃^*

x₂^* x₁^*

x x₃^*

xxx ∆q₁

q₀₂ q₂ C₁

q₁

б)

q₂ q₂

q_max

q₂₂ x₂^* q₂₀

x₁^*

q₁ q₁₀ q_max q₁

q₁

в) г)

Рис.19. Ілюстрація методів розв’язку багатокритеріальних задач: а) оптимізація

по одному „суперкритерію”; б) метод поступок; в) завдання рівнів претензій;

г) знаходження паретовської множини альтернатив.

Дата добавления: 2014-01-07