Опис вибору на мові бінарних відношень

Знаходження множини Парето

Четвертий спосіб багатокритеріального вибору, що повністю формалізується, полягає у відмові від виділення єдиної „найкращої” альтернативи та погодження із тим, що перевага одній альтернативи над другою може віддаватися тільки тоді, коли перша по усім критеріям краще другої. Якщо ж перевага хоча б по одному критерію розходиться із перевагою по другому, то такі альтернативи признаються непорівнянними. У результаті попарного порівняння альтернатив всі гірші по всім критеріям альтернативи відкидаються, а решта, що залишилися, непорівнянні між собою (не домінуючі), приймаються. Якщо всі максимально досяжні значення часткових критеріїв не відносяться до однієї й тієї ж альтернативи, то прийняті альтернативи створюють множину Парето (Парето (Pareto) Вильфредо (1848 – 1923) італійський економіст та соціолог, один із засновників функціоналізму) і вибір на цьому закінчується. На Рис.19 г) жирною лінією виділено множину Парето для даного прикладу. При необхідності ж вибору єдиної альтернативи залучають додаткові міркування: вводять нові, додаткові критерії та обмеження, кидають жеребок, звертаються до експертів.

Друга, більш загальна мова - це мова бінарних відношень. Її більша загальність, ніж у критеріальної мови, основана на врахуванні факту, що у реальності дати оцінку окремо взятій альтернативі часто важко або неможливо. Однак якщо розглядати її не окремо, а у парі з другою альтернативою, то знаходяться підстави вказати, якій із них віддати перевагу.

Основні припущення цієї мови зводяться до наступного:

Ø окрема альтернатива не оцінюється, тобто критеріальна функція не вводиться;

Ø для кожної пари альтернатив (x, y) деяким чином можна встановити, що одній із них можна віддати перевагу, або вони рівноцінні, або непорівнянні (часто два останні поняття ототожнюються);

Ø відношення переваги усередині довільної пари альтернатив не залежить від інших пред’явлених до вибору альтернатив.

Математично бінарне відношення R на множині X визначається як деяка підмножина впорядкованих пар (x, y). Зручно користуватися позначенням xRy, якщо x знаходиться у відношенні R з y, та x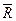y у протилежному випадку. Множина всіх пар 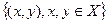називається повним („універсальним”) бінарним відношенням. Оскільки у загальному випадку не всі можливі пари (x, y) задовольняють умовам, що накладаються відношенням R, то бінарне відношення є деякою підмножиною повного бінарного відношення, тобто R.

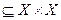Задати відношення – це значить тим чи іншим способом вказати всі пари (x, y), для яких виконане відношення R.

Існує чотири способи завдання відношень; переваги кожного виявляються при різних характеристиках множини X.

Перший, очевидний, спосіб полягає у безпосередньому перерахуванні таких пар. Ясно, що він припустимий лише у випадку скінченої множини X.

Другий зручний спосіб завдання відношення R на скінченій множині – матричний. Всі елементи нумеруються, і матриця відношення R визначається своїми елементами α_ij (R)= {1: x_iRx_j; 0: x_i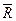x_j } для всіх i та j. Відомим прикладом такого завдання відношення є турнірні таблиці (якщо нічиї позначити нулями, як і програші, то матриця зобразить відношення „“ x_i - переможець x_j “).

Третій спосіб – завдання відношення графом. Вершинам графа G (R) ставлять у відповідність (пронумеровані) елементи множини X, і якщо x_iRx_j, то від вершини x_i проводять спрямовану дугу до вершини x_j; якщо ж x_i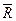x_j, то дуга відсутня.

Для визначення відношень на безкінечних множинах використовують четвертий спосіб – завдання відношення R перерізами. Множина R⁺ (x) = 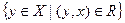називається верхнім перерізом відношення R, а множина R^- (x) = 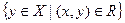нижнім перерізом. Інакше кажучи, верхній переріз – це множина всіх y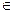X, що знаходяться у відношенні yRx із заданим елементом x 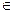X, а нижній переріз – множина всіх y 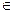X, з якими заданий елемент x знаходиться у відношенні R. Відношення однозначно визначається одним із своїх перерізів.

Дата добавления: 2014-01-07