Відношення еквівалентності, порядку та домінування

Для теорії вибору особливе значення серед всіх бінарних відношень мають відношення, котрі відповідають перевазі однієї альтернативи над другою, або випадку, коли неможливо віддати перевагу жодній альтернативі. Ці відношення задають через відношення еквівалентності, порядку та домінування. Бінарне відношення R на множині X є:

· рефлексивне, якщо xRx для кожного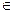 xX;

· анти рефлексивне, якщо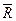 xxx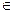X (тобто R може виконуватися лише для не співпадаючих елементів);

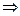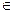· симетричне, якщо xRyyRxx, yX;

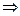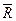· асиметричне, якщо xRyyxx, y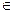X (ясно, що асиметричне відношення R анти рефлексивне);

· анти симетричне, якщо для всіх x, y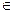X (xRy, yRx) 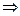x = y;

· транзитивне, якщо для всіх x, y, z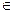X (xRy, y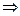Rz) xRz;

· від’ємно транзитивне, якщо відношення 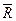транзитивне;

· сильно транзитивне, якщо відношення R одночасно транзитивне та від’ємно транзитивне.

Відношення R на множині X, називається відношенням еквівалентності (позначається ~), якщо воно рефлексивне, симетричне та транзитивне. Завдання відношення еквівалентності тотожне розбиттю множини X на непересічні класи (X = 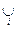X_і, X_i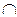X_j = Ø при i ≠ j) еквівалентних елементів: x ~ y тоді й тільки тоді, коли x, y X (тобто x та y належать одному класу еквівалентності).

Відношенням нестрогого порядку (позначається 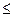) називається рефлексивне, антисиметричне та транзитивне відношення. Відношенням строгого порядку (позначається <) називається анти рефлексивне, асиметричне та транзитивне відношення. Відношення нестрогого порядку можна розглядати як об’єднання відношень < та ~.

Нарешті, відношенням домінування називається відношення, що володіє анти рефлексивністю та анти симетричністю. Кажуть, що „ x домінує y ” (позначається x >> y), коли x в якомусь смислі перевершує y. (Очевидно, що строгий порядок це частковий випадок домінування, при якому має місце ще й транзитивність).

Деякі особливості вибору привели до побудови третьої, ще більш загальної мови його описання. Нерідко стикаються з ситуаціями, коли переваги між двома альтернативами залежать від решти альтернатив. Наприклад, перевага покупця між чайником та кавоваркою залежить від наявності у продажу млинка для кави.

Дата добавления: 2014-01-07