Операції над множинами

Розглянемо дві множини А та В і введемо кілька операції над ними. Для графічної ілюстрації будемо використовувати так звані діаграми Венна або кола Ейлера. Діаграма Венна являє собою схемне зображення множин у вигляді множин точок: універсум U зображується множиною точок деякого прямокутника, а його підмножини – у вигляді кіл або інших простих областей у цьому прямокутнику.

Означення 1.5. Об’єднання А і В (АÈВ) – множина, що складається з усіх елементів множин А, всіх елементів множини В і не містить ніяких інших елементів (рис 1.1,а), тобто

АÈВ = { x | x ÎA або x ÎВ}.

Наприклад, {1,2,3}È{2,3,4} = {1,2,3,4}.

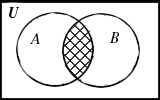
Означення 1.6. Переріз (перетин)А і В (АÇВ) – множина, що складається з тих і тільки тих елементів, які належать одночасно множині А та множині В (рис 1.1,б), тобто

АÇВ = { x | x ÎA та x ÎВ}.

Наприклад, {1,2,3}Ç{2,3,4} = {2,3}.

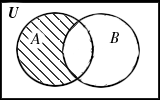
Означення 1.7. Різниця А і В або відносне доповнення В до А (А-В, A\B) – множина, що складається з тих і тільки тих елементів, які належать множині А та не належать множині В (рис 1.1,в), тобто

А\В = { x | x ÎA та x ÏВ}.

Наприклад, {1,2,3}\{2,3,4} = {1}.

Означення 1.8. Симетрична різниця (диз’юнктивна сума) А і В (А¸В, AÅB) – множина, що складається з усіх елементів А, які не належать множині В, й усіх елементів В, які не належать множині А (рис 1.1,г), тобто

А¸В = { x | (x ÎA та x ÏВ} або (x ÏA та x ÎВ)).

За означенням: А¸В = (А\В)È(В\А).

Наприклад, {1,2,3}¸{2,3,4} = {1,4}.

Означення 1.9. Абсолютне доповнення або просто доповнення А (А’, 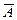) – множина, що містить усі елементи універсуму, за винятком елементів А (рис 1.1,д), тобто

А’ = { x | x ÏA).

За означенням: А’ = U \А.

а	б	в
г	д

Рис 1.1. Діаграми Венна.

(а – об’єднання, б – перетин, в – різниця, г – симетрична різниця, д – доповнення)

Операції над множинами, як і операції над числами, мають деякі властивості. Останні виражаються сукупністю тотожностей незалежно від конкретного вмісту множин, що входять у них, і є підмножинами деякого універсуму U.

Для будь-яких множин А, В та С справедливі наступні властивості:

§ ідемпотентність (самопоглинання)

1а) AÈA = A 1б) AÇA = A

§ комутативність

2а) AÈB = BÈA 2б) AÇB = BÇA

§ асоціативність

3а) AÈ(BÈC) = (AÈB)ÈC 3б) AÇ(BÇC) = (AÇB)ÇC

§ дистрибутивність

4а) AÈ(BÇC) = (AÈB)Ç(AÈC) 4б) AÇ(BÈC) = (AÇB)È(AÇC)

§ властивості Æ та U

5а) AÈÆ = A 5б) AÇÆ = Æ

6а) AÈA’ = U 6б) AÇA’ = Æ

7а) AÈ U = U 7б) AÇ U = A

8а) Æ’ = U 8б) U ’ = Æ

§ поглинання

9а) AÈ(AÇB) = A 9б) AÇ(AÈB) = A

§ закони де Моргана

10а) (AÈB)’ = A’ÇB’ 10б) (AÇB)’ = A’ÈB’

§ властивості доповнення, різниці та рівності

11) AÈB = U & AÇB = Æ Û B = A’

12) A’’ = A (інволютивність)

13) A\B = AÇB’

14) A¸B = (AÇB’) È(A’ÇB)

15) A¸B = B¸A

16) (A¸B)¸C = A¸(B¸C)

17) A¸Æ = ƸA = A

18) AÌB Û AÇB = A Û AÈB = B Û AÇB’ = Æ

19) A=B Û (AÇB’)È(A’ÇB) = Æ

Доведення цих співвідношень можна ґрунтувати на означенні 1.3 та лемі 1.1, або доводити за допомогою побудови діаграм Венна для лівої та правої частин співвідношень.

Доведемо, наприклад, співвідношення 3б: AÇ(BÇC) = (AÇB)ÇC. Нехай x ÎAÇ(BÇC) Þ x ÎA, x ÎB, x ÎC Þ x Î(AÇB) і x ÎC Þ x Î(AÇB)ÇC і AÇ(BÇC)Í(AÇB)ÇC. Одержання оберненого включення виконується аналогічно.

Тепер наведемо доведення для 4а: AÈ(BÇC) = (AÈB)Ç(AÈC). З одного боку, оскільки (BÇC) Í B, то AÈ(BÇC) Í AÈВ. Аналогічно BÇC Í C і AÈ(BÇC) Í AÈC. Значить, AÈ(BÇC) Í (AÈB)Ç(AÈC). З іншого боку, якщо x Î(AÈB)Ç(AÈC), то x ÎAÈB і x ÎAÈC. Якщо x ÎA, то x ÎAÈ(BÇC). А якщо x ÏA, то x ÎB і x ÎC і тоді x ÎBÇC. Отже, (AÈB)Ç(AÈC)Í AÈ(BÇC). Разом з отриманим раніше включенням маємо потрібну рівність.

Доведемо співвідношення 1а: AÈA = A.

AÈA = (AÈA)Ç U = (AÈA)Ç(AÈA’) = AÈ(AÇA’) = AÈÆ = A.

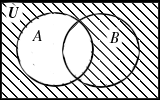
Доведемо співвідношення 10а: (AÈB)’ = A’ÇB’ за допомогою діаграм Венна. Спочатку побудуємо діаграму для (AÈB)’ – рис. 1.2, а. Множині A’ відповідає рис. 1.2, б. Множині В’ – рис. 1.2, в. Множині A’ÇB’ відповідають частини, які заштриховані на рис. 1.2 б, в. Ця множина зображена на рис. 1.2, г.

	а
б	в	г

Рис. 1.2. Діаграми Венна для доведення співвідношення (AÈB)’ = A’ÇB’.

(а - (AÈB)’, б - A’, в - В’, г - A’ÇB’).

Отримали, що множини (AÈB)’ та A’ÇB’ однаково зображуються на діаграмах Венна, тобто (AÈB)’ = A’ÇB’.

Доведення інших властивостей залишаємо читачеві на самостійну роботу. ►

Із властивостей комутативності й асоціативності операції об’єднання випливає, що об’єднання кількох множин можна виконати, послідовно об’єднуючи їх, причому порядок входження множин не впливає на результат. Отже об’єднання сукупності множин можна подати співвідношенням

А₁ È А₂ È... È А_n = .

Аналогічно на n множин узагальнюється операція перерізу:

А₁ Ç А₂ Ç... Ç А_n = .

Використовуючи узагальнення операцій об’єднання та перерізу на n множин, можна узагальнити також інші співвідношення, наприклад, закон де Моргана, який в узагальненому вигляді має вигляд:

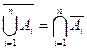і .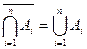

Означення 1.10. Сукупність множин А₁, А₂,..., А_n називається розбиттям множини А, якщо:

1. = А.

2. А _і Ç А _j = Æ, " i ¹ j.

Якщо умова 2 не задовольняється, то сукупність множин буде називатися покриттям.

Наприкінці цієї лекції наведемо приклади використання тотожностей 1-19 для спрощення складних виразів, які містять множини, аналогічно тому, як проводяться спрощення виразів в елементарній алгебрі.

1. (AÇBÇC) È (A’ÇBÇC) È B’ È C’ =

= [(AÈA’) Ç B Ç C] È B’ È C’ = (4б)

= (U Ç B Ç C) È B’ È C’ = (6a)

= (B Ç C) È B’ È C’ = (7б)

= (B Ç C) È (B Ç C)’ = (10б)

= U (6a)

2. (AÇBÇCÇD’) È (A’ÇC) È (B’ÇC) È (CÇD) =

= (AÇBÇCÇD’) È [(A’ÈB’ÈD) ÇC] = (4б)

= (AÇBÇCÇD’) È [(AÇBÇD’)’ ÇC] = (10б)

= [(AÇBÇD’) È (AÇBÇD’)’] Ç C = (4б)

= U Ç C = (6a)

= C (7б)

3. (AÇB’)’ È B =

= (A’ÈB’’) È B = (10б)

= (A’ÈB) È B = (12)

= A’ È (BÈB) = (3a)

= A’ È B (1a)

Дата добавления: 2014-01-07