Знаходження оберненої матриці за допомогою визначників

Знайдемо умову оборотності квадратної матриці А порядка n, тобто умову існування такої матриці 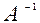, для якої .

Квадратну матрицю називають невиродженою, якщо її визначник не дорівнює 0.

Теорема 5.1. (критерій оборотності матриці). Матриця буде мати обернену тоді і тільки тоді, коли вона невироджена.

Доведення. Необхідність. За означенням, → , тобто матриця А – невироджена.

Достатність. Нехай . Покажемо, що вона має обернену.

Доведемо, що , де

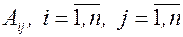, - алгебраїчні доповнення елементів матриці А.

З властивостей визначників слідує, що

Отже, . Аналогічно доводимо, що .

Можна записати . Доведено.

Матрицю називають приєднаною до матриці А.

На цій теоремі грунтується метод приєднаної матриці знаходження оберненої матриці.

Схема метода приєднаної матриці.

Крок 1. Обчислюємо визначник матриці А.

Крок 2. Якщо detA =0, то обернена матриця не існує.

Якщо detA ≠0, то будуємо приєднану матрицю .

Крок 3. Обернену матрицю знаходимо за формулою .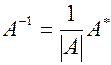

Зауваження. Правильність обчислень перевіряється умовою .

Приклад 5.1. Знайти матрицю обернену заданій методом приєднаної

матриці.

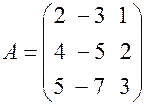
Дата добавления: 2014-01-07