Лекція№10.Диференціальне числення функцій однієї змінної

1. Задачі, що приводять до поняття похідної. Означення похідної. Механічний, фізичний та геометричний зміст похідної

2. Рівняння дотичної до графіка функції. Рівняння нормалі до графіка функції

3. Диференціювання функцій

4. Таблиця похідних

5. Похідна вищих порядків

6. Теореми диференціального числення

1. Задачі, що приводять до поняття похідної. Означення похідної. Механічний, фізичний та геометричний зміст похідної

Задачі, що приводять до поняття похідної:

1) Задача про швидкість прямолінійного руху

2) Задача про густину неоднорідного тіла

3) Задача про силу струму

4) Задача про теплоємність

5) Задача про швидкість хімічної реакції

6) Задача про дотичну до кривої

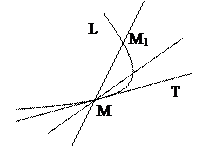
Розглянемо криву L і на ній точки M і M₁.

Пряму MM₁, що проходить через ці точки, називають січною. Нехай точка M₁, рухаючись вздовж кривої, наближається до точки M. Тоді січна MM₁ повертатиметься навколо точки M, а довжина відрізка ММ₁ прямуватиме до нуля.

Якщо при цьому і величина кута М₁МТ прямує до нуля, то пряму МТ називають граничним положенням січної ММ₁.

Пряму МТ, яка є граничним положенням січної ММ₁, називають дотичною до кривої L в точці М.

Якщо січна ММ₁ наближається до різних прямих або взагалі не наближається ні до якої прямої, то вважають, що в точці М дотичної не існує.

Розглянемо випадок, коли крива в прямокутній системі координат задана рівнянням 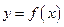і має в точці 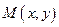не вертикальну дотичну. Розглянемо задачу про знаходження кутового коефіцієнта цієї дотичної. Надамо аргументу 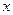приросту 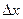: тоді значенню 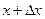відповідатимуть значення функції 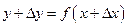і точка на кривій.

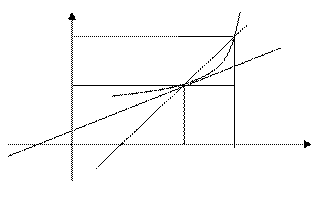
Проведемо січну ММ₁ і позначимо через кут, утворений цією січною з додатним напрямом осі Ох. З графіка видно, що кутовий коефіцієнт січної ММ₁ дорівнює:

.

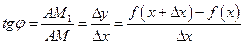Якщо , то точка М₁ прямує до точки М вздовж кривої 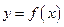, а січна ММ₁, повертаючись навколо точки М, переходить в дотичну МТ. Кут при цьому прямує до деякого граничного значення 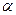. Отже, кутовий коефіцієнт дотичної дорівнює

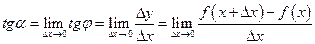
Нехай на деякому проміжку 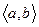задано функцію 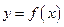. Візьмемо будь-яку точку 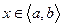і надамо 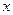довільного приросту 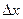такого, щоб точка 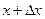також належала проміжку 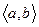. Знайдемо приріст функції: .

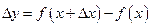Похідною функції 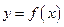в точці 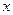називається границя відношення приросту функції 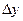в цій точці до приросту аргументу 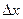, коли приріст аргументу прямує до нуля.

Похідна функції 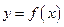в точці 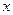позначається одним із символів:

.

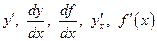За означенням .

Якщо в деякій точці 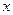границя 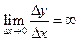, то похідну 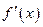в цій точці називають нескінченною.

Якщо границя 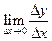в деякій точці 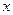не існує, то не існує в цій точці і похідної .

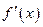Значення похідної функці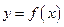ї точці 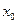позначається одним із символів .

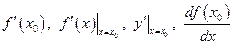Операція знаходження похідної від функції 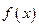називається диференціюванням цієї функції.

Механічний зміст похідної: швидкість в даний момент часу – це похідна від пройденого шляху 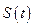за часом .

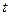Фізичний зміст похідної: якщо функція 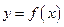описує деякий фізичний процес, то похідна є швидкістю зміни цього процесу.

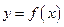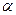Геометричний зміст похідної: кутовий коефіцієнт дотичної до кривої в точці або тангенс кута , що утворює дотична до кривої в даній точці з додатним напрямом осі Ох – це похідна 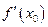в цій точці: .

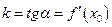2. Рівняння дотичної до графіка функції. Рівняння нормалі до графіка функції

Рівняння дотичної до кривої 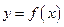в точці : .

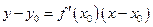Якщо функція в точці 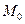має нескінченну похідну, то дотична в цій точці паралельна осі Оу, а її рівняння .

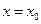Нормаллю до кривої називається пряма, що проходить через точку дотику, перпендикулярно до дотичної.

Рівняння нормалі до кривої 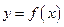в точці : .

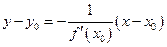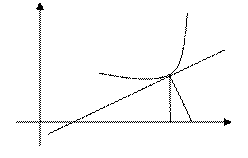
Довжина відрізка 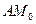називається довжиною відрізка дотичної.

Довжина відрізка 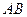називається піддотичною.

Довжина відрізка 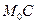називається довжиною відрізка нормалі.

Довжина відрізка називається піднормаллю.

3. Диференціювання функцій

Функція 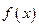називається диференційовною в точці 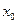, якщо в цій точці вона має похідну .

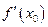Функція 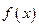називається диференційовною на проміжку, якщо вона диференційовна в кожній точці цього проміжку.

Дата добавления: 2014-01-07