
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Інтерполяція для випадку рівновіддалених вузлів
|
|
|
|
Вузли називаються рівновіддаленими, якщо відрізок [ x0, xn ] поділений точками xi на n рівних частин:  . Для невузлових точок i було б нецілим, але натомість вводиться величина
. Для невузлових точок i було б нецілим, але натомість вводиться величина  , яка є відстанню від x до x0 в одиницях h. Тоді
, яка є відстанню від x до x0 в одиницях h. Тоді  .
.
Кінцевими різницями функції y=y(х) називаються різниці виду:
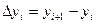 – кінцеві різниці 1-го порядку;
– кінцеві різниці 1-го порядку;
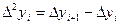 – кінцеві різниці 2-го порядку;
– кінцеві різниці 2-го порядку;
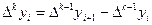 – кінцеві різниці k -го порядку.
– кінцеві різниці k -го порядку.
В залежності від розташування досліджуваної точки відносно відомих, заданих таблично, кращі наближення дають різні інтерполяційні багаточлени, побудовані з використанням кінцевих різниць.
Інтерполяційні формули Ньютона
Для інтерполяції та екстраполяції в точках x, близьких до початку таблиці, використовується перша інтерполяційна формула Ньютона, яка має вигляд:

або 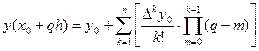 .
.
де m=2i-1, q=(x-x0)/h.
В ній використовується рядок NI таблиці різниць:
| x | y | Dy | D2y | D3y | D4y | |
| x0 |  y0 y0
| Dy0 | D2y0 | D3y0 | D4y0 | N1 |
| x1 | y1 | Dy1 | D2y1 |  D3y1 D3y1
|  D4y1 D4y1
| N2 |
| x2 | y2 | Dy2 |  D2y2 D2y2
| D3y2 | ||
| x3 | y3 |  Dy3 Dy3
| D2y3 | |||
| x4 |  y4 y4
| Dy4 | ||||
| x5 | y5 |
Таблиця 1. Горизонтальна таблиця кінцевих різниць при і=5
При n=1 і n=2 з цієї формули одержуємо часткові випадки:
лінійна інтерполяція 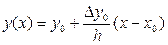 ,
,
квадратична інтерполяція  .
.
Якщо точка інтерполювання лежить поблизу кінцевої точки xn таблиці або десь справа від неї, вузли треба брати в порядку xn, xn-h, xn-2h,.... Тоді формула набуде вигляду:
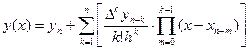 або
або 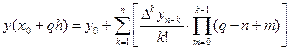 .
.
Це – друга інтерполяційна формула Ньютона. В ній використовується нижній похилий рядок таблиці 1.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 377; Нарушение авторских прав?; Мы поможем в написании вашей работы!