Граничные условия для векторов ЭМП

**для магнитного самостоятельно**

1. Нормальные составляющие

Соотношения, показывающие связь между значениями векторов ЭМП в разных средах, у поверхности раздела называют граничными условиями. (Используют интегральную запись уравнений Максвелла). На поверхности раздела двух сред с параметрами соответственно, выделим малый элемент 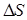так чтобы:

1. его можно считать плоским;

2. распределение Dn в пределах 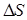должно быть равномерным.

Построим на 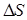цилиндр с основаниями в разных средах. Используем третье уравнение Максвелла:

.

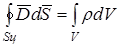Поверхность цилиндра:

.

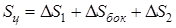Устремим так, чтобы 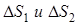оставались в разных средах:

;

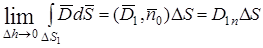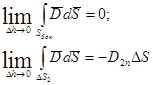
Если заряд не сосредоточен на поверхности раздела, то:

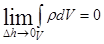
и нормальная компонента вектора 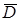непрерывна при переходе из одной среды в другую. Если заряд распределен по поверхности раздела в виде бесконечно тонкого слоя с поверхностной плотностью:

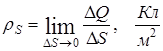
тогда 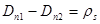, то есть нормальная компонента вектора D претерпевает скачек на величинуповерхностного заряда. Для вектора Е:

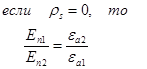
Нормальная компонента Е претерпевает разрыв. На самом деле поверхностных зарядов не бывает, толщина слоя конечна и D меняется постепенно. Но математическая модель удобнее.

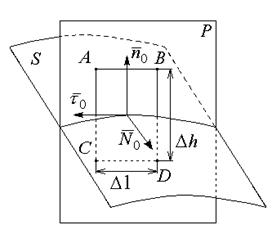
2. Тангесальные составляющие

Из произвольной точки на поверхности S раздела двух изотропных сред проведем единичную нормаль n₀. Через нее проведем плоскость Р и на линии пересечения Р и S выделим малый отрезок D l такой, чтобы считать его прямолинейным и `E неизменной в его пределах.

На отрезке Dl построим контур ABCD высотой Dh

`- касательная к D l,

- нормаль к P, образующий правовинтовую систему с ABCD и .

Используем второе уравнение Максвелла:

,

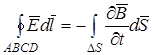где

.

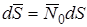Левую часть представим в виде суммы четырех интегралов:

и оставляя AB и CD в разных средах, устремляем Dh ® 0:

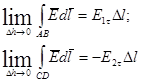
Так как Е и конечные величины, то:

.

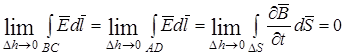А , то есть касательная, составляющая вектора Е, непрерывна при переходе через границу раздела двух сред.

Полная система граничных условий:

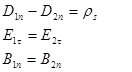
где 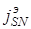- плотность поверхностного тока, направленного ортогонально вектору 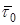(или его составляющая).

На поверхности раздела с идеальным проводником 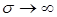, внутри которого поле отсутствует, согласно уравнению Максвелла будут справедливы следующие граничные условия:

,

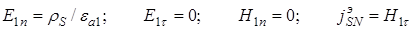или для Н в векторной форме:

Падение плоских электромагнитных волн на границу раздела двух сред

Границу раздела будем полагать бесконечно протяженной. Плоскость, проходящая через нормаль к границе раздела параллельно направлению распространения, называют плоскостью падения.

Если вектор Е перпендикулярен этой плоскости, то волна – нормально поляризованная, если параллелен, волна – параллельно поляризованная.

Любую другую ориентацию вектора Е следует рассматривать как суперпозицию .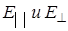

Дата добавления: 2014-01-06