Логический вывод

Геометрический смысл произвольной t – нормы

Из аксиом T1(0) и T2(0) что область определения x1 T x2 находится на стороне единичного куба в плоскости (x1;x2), другими словами из аксиомы T1(0) следует, что на стороне x2 = 1, единичного куба образуется линия x1 Т x2 = x1, а на стороне x2 = 0 или в плоскости x1 T x2 = 0.

Если использовать семетричность T2(0), то на стороне x1=1 образуется линия x1 T x2 = x2, а на стороне x1 = 0 образуется линия x1 T x2 = x2

Таким образом значения x1 T x2 в четырёх вершинах еденичного куба, явл-ся также значениями чёткой операции «И». Из аксиомы T2 следует что график симметричен относительно плоскости образованной наклонными x1 = x2.

рис 4

3) нечёткое ррашрнение «ИЛИ» - t – конорма (треугольная конорма или s – норма).

s – нормой называется бинарная операция G: [0;1]x[0;1]->[0;1] удовлетворяющие следующим аксиомам:

S1(0): граничные условия

фор 5

типичной S – нормой называется операция максимума «сим1»

Приближенные рассуждения (логический вывод)

Под приближёнными рассуждениями понимается процесс при котором из нечётких посылок получают некоторые следствия, возможно тоже нечёткие. Приближённые рассуждения лежат в основе способности человека понимать естественный язык; разбирать подчерк; играть в игры, требующие умственных усилий, в общем, принимать решения в сложной и не полностью определённой среде. Это отличает человека от интеллекта вычислительной машины.

В классической Булевой логике логический вывод базируется на следующих тафтологиях:

- модус поненс (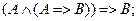

- модус толленс

- силлогизм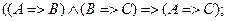

- контрапозиция

наиболее часто употребляется «модус поненс» его можно записать в виде таблицы:

Посылка	A есть истинно
Импликация	Если A, то B истинно
Логический вывод	B есть истинно

В нечёткой логике известно, что близкое к A утверждение сим2 яв-ся истинным, модус понненус не может быть применён.

В нечёткой логике главным инструментом яв-ся композиционное правило Заде. Оно формулируется следующим образом:

Пусть U и V - два универсальных множества, с базовыми переменными u принадлежит U, v принадлежит V.

A и F – нечёткие подмножества U и UxV

Тогда из нечётких множеств A и F, следует множество фор6

нечёткий логический вывод происходит за 4 шага:
1) Фаззификация – с помощью фун-ии принадлежности всех термов входных лингвистических переменных и на основании задаваемых чётких значений из универсумов (универсальных множеств), входных лингвистических переменных, определяется степень уверенности в том выходная лингвистическая переменная принимает конкретные значения.

2) Этап непосредственного нечёткого вывода – на основании набора правил (нечёткой базы знаний) вычисляются значения истинности для предпосылок всех правил на основании конкретных нечётких операций, соответствующих конъюнкции или дизъюнкции термов в левой части правил.

3) Этап композиции (агрегации, аккумуляции) – все нечёткие множества назначенные для каждого терма, каждой выходной лингвистической переменной объединяются вместе и формируется единственное нечёткое множество – значение для каждой выводимой лингвистической переменной.

4) Этап дефаззификации – этот этап не обязателен, он используется, когда полезно преобразовать нечёткий набор значений выводимых лингвистических переменных к точным значениям.

Существуют алгоритмы нечёткого логического вывода:

1) Алгоритм Mamdani

2) Алгоритм Tsukamoto

3) Алгоритм Larsen

Дата добавления: 2014-01-06