Гидравлика 2 страница

Среди аномальных (ненъютоновских) жидкостей существуют такие (например, бингамовская жидкость), в которых, при уменьшении скорости сдвига до определенного значения, касательное напряжение сохраняет постоянное отличное от нуля предельное значение. Наиболее общими свойствами текучести жидкостей занимается специальная область механики сплошных сред - реология.

При изучении потоков жидкостей и газов обычно рассматривается перенос трех величин: одной векторной (количества движения) и двух скалярных (тепла и вещества). В движущемся потоке, в общем случае, наблюдается неоднородность таких величин, как скорость, температура и концентрация вещества. Вследствие наличия этих неоднородностей в среде возникают явления переноса количества движения, тепла и массы.

Если в потоке выделить некоторый элементарный объем, то по его поверхности будут действовать касательные и нормальные силы. Касательные силы возникают вследствие наличия внутреннего трения или вязкости. Как известно из физики, Ньютон сформулировал закон, согласно которому касательное напряжение трения между двумя слоями прямолинейно движущейся вязкой жидкости пропорционально отнесенному к единице длины изменению скорости по нормали к направлению движения

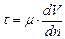. (2.11)

Коэффициент пропорциональности 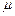в уравнении (2.11) называется динамическим коэффициентом вязкости.

Закон Ньютона позже был получен в кинетической теории газов как закон переноса количества движения молекул.

Из уравнения (2.11) видно, что когда 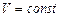, перенос количества движения отсутствует и касательное напряжение равно нулю, т.е. .

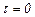Динамический коэффициент вязкости не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и ее температурой.

Вязкость есть свойство, противоположное текучести: более вязкие жидкости (глицерин, смазочные масла и др.) являются менее текучими, и наоборот. При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью (рис. 2.2).

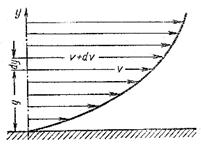
Рис. 2.2. Профиль скоростей при течении вязкой

жидкости вдоль стенки

Скорость V уменьшается по мере уменьшения расстояния y от стенки вплоть до V = 0 при y = 0, а между слоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений (напряжении трения).

Из закона трения следует, что напряжения трения возможны только в движущейся жидкости, т.е. вязкость жидкости проявляется лишь при ее течении. В покоящейся жидкости касательные напряжения равны нулю. В системе СГС за единицу вязкости принимается пуаз: 1 П = 1 дин с/см² = 0,1 Па.с = 0,0102 кГс с/м².

Наряду с динамической вязкостью m применяют кинематическую n = m / r. Единицей измерения кинематической вязкости является стокс: 1 Ст = 1 .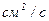

Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней (рис. 2.3).

Вязкость газов, наоборот, с увеличением температуры возрастает. Объясняется это различием природы вязкости в жидкостях и газах. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с увеличением температуры уменьшаются, поэтому вязкость падает. В газах же

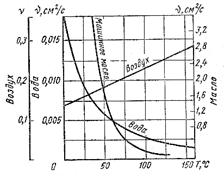
Рис. 2.3. Зависимость кинематической вязкости

от температуры

вязкость обусловлена, главным образом, беспорядочным тепловым движением молекул, интенсивность которого увеличивается с повышением температуры. Поэтому вязкость газов с увеличением температуры возрастает. Вязкость жидкостей зависит также от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления (в несколько десятков МПа). С увеличением давления вязкость большинства жидкостей возрастает.

Влияние температуры на вязкость жидкостей можно оценить формулой

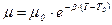, (2.12)

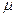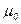где и - вязкости при температуре 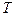и ;

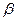- коэффициент, значение которого для масел изменяется в пределах 0,02 - 0,03.

Вязкость жидкостей также зависит от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления (в несколько десятков МПа). С увеличением давления вязкость большинства жидкостей возрастает, что может быть оценено формулой

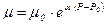, (2.13)

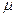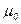где и - вязкости при давлении р и ;

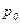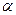- коэффициент, значение которого для минеральных масел изменяется в пределах 0,02 - 0,03 (нижний предел соответствует высоким температурам, а верхний - низким).

Приближенная зависимость относительной вязкости от давления для минеральных масел для предельных значений коэффициента 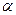показана на рис. 2.4.

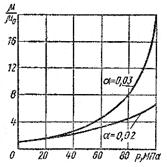
Рис. 2.4. Зависимость относительной вязкости

минерального масла от давления

Вязкость становится существенной при движении сплошной среды со значительными скоростями ее деформации. Характер движения вязкой жидкости зависит от соотношения между скоростью потока, линейным размером обтекаемого тела или русла и коэффициентом вязкости среды (число Рейнольдса).

Удельная теплоемкость (или просто теплоемкость) - это количество теплоты, которое необходимо подвести к единице количества вещества в заданном процессе, чтобы изменить его температуру на 1 градус. Из определения теплоемкости следует

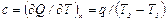, (2.14)

где q - теплота, подведенная к телу;

- изменение температуры тела.

Теплота q зависит не только от начального и конечного состояния системы, но и от характера процесса. Следовательно, теплоемкость также должна зависеть от характера процесса. В процессе, происходящем при постоянном объеме (изохорном), работа равна нулю, а вся теплота расходуется на увеличение внутренней энергии системы:

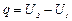, (2.15)

и подставив это выражение в уравнение (2.14), получим:

. (2.16)

Теплоемкость в этом случае называют изохорной.

В процессе, где постоянное давление (изобарном), подведенная теплота идет на увеличение внутренней энергии и совершение работы над внешними силами: 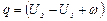, где 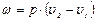. Следовательно,

. (2.17)

Выражения, стоящие в скобках, - это энтальпии 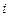, поэтому 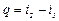. Теплоемкость при этом называют изобарной.

. (2.18)

Эксперименты показывают, что 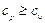. Для идеальных газов, молекулы которых находятся в состоянии хаотического движения и лишены сил взаимодействия, соотношение между теплоемкостями и подчиняется уравнению Майера

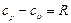, (2.19)

где R - газовая постоянная. Величина носит название коэффициента Пуассона.

Теплоемкости и являются функциями температуры и давления тела в любом из его агрегатных состояний. Зависимость теплоемкостей газов от давления наиболее резко выражена вблизи кривой насыщения, в области критической точки, а также в сверхкритической области. У жидкостей величина давления существенно влияет на теплоемкость только вблизи кривой насыщения и особенно в критической области. При больших давлениях обнаруживается зависимость теплоемкости жидкостей от давления, причем с ростом давления теплоемкость сначала обычно уменьшается, достигает минимума, а затем увеличивается.

Теплоемкость жидкостей всегда выше, чем теплоемкость газов при той же температуре, при этом температурная зависимость теплоемкости жидкостей выражена менее резко по сравнению с газами. Значение коэффициента Пуассона k у жидкостей всегда меньше, чем у газов. При температуре абсолютного нуля теплоемкости всех веществ в жидком и твердом состояниях обращаются в нуль.

Если в точках пространства, заполненного твердыми, жидкими или газообразными физическими телами, в некоторый момент времени имеют место различные температуры, то от точек с более высокими температурами тепло будет переноситься к точкам с более низкими температурами. При этом процесс переноса тепла может осуществляться тремя путями: теплопроводностью, конвективным теплообменом и радиацией.

Теплопроводностью, или кондукцией, называется процесс передачи тепла при непосредственном соприкосновении частиц тела, имеющих разные температуры, при этом тепло передается от одной молекулы к другой. Таким процессом передачи тепла полностью объясняется процесс переноса тепла в твердых телах и частично в жидкостях и газах. В покоящихся и движущихся жидкостях и газах молекулы, не занимая фиксированного положения и непрерывно перемещаясь, также передают тепло от молекулы к молекуле.

Кроме того, в жидкостях и газах перенос тепла осуществляется перемещением макрочастиц жидкостей и газов. Размеры этих частиц во много раз превосходят размеры молекул. Такой процесс называется конвективным теплообменом. Обычно различают два типа конвективного теплообмена: естественная конвекция и вынужденная.

Естественной конвекцией будем называть такой перенос, при котором перемещение жидкостных и газообразных частиц, несущих тепло, вызывается лишь только действием разности плотностей среды, обычно возникающей из-за наличия разности температур. Когда перемещение частиц жидкости и газа, переносящих тепло, происходит не под воздействием разности плотностей, а как результат вынужденного движения (например, вентилятором), конвекция называется вынужденной.

Радиацией называется процесс переноса тепла путем излучения и поглощения тепловой энергии в форме электромагнитных волн. Перенос тепла радиацией может производиться твердыми, жидкими и газообразными телами. Природа и закономерности радиационного переноса такие же, как и для любых других электромагнитных волн (радио, свет, рентгеновские лучи). Все они отличаются лишь длиной волны. Тепловые излучения - это электромагнитные волны длиной 0,76-400 мк, в то время как видимые человеческим глазом световые лучи имеют длину волны 0,35-0,75 мк.

Если поверхности равных температур в некотором пространстве назвать изотермическими, то общее количество тепла Q, проходящего через площадку, составляющую часть изотермической поверхности с площадью s, за время t будет равно, согласно закону переноса Фурье,

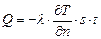, (2.20)

где Т - температура;

n - нормаль к площадке;

- коэффициент теплопроводности.

Количество тепла q, проходящего через единицу площади в единицу времени, будет равно

. (2.21)

Коэффициент теплопроводности имеет размерность в системе единиц СИ - .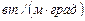

Величина для разных веществ существенно различна и ее значение зависит от температуры. Лучшими проводниками тепла являются металлы, хуже всех проводят тепло газы.

Теплопроводность металлов с повышением температуры убывает. Исключением является алюминий, для которого теплопроводность не зависит от температуры. Для воздуха, водорода и других газов, наоборот, теплопроводность с повышением температуры растет.

Коэффициенты теплопроводности большинства жидкостей уменьшаются при повышении температуры, исключением является вода.

В практических расчетах при конвективном переносе количество тепла, переносимого от поверхности обтекаемого тела, имеющей температуру 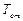, в поток с температурой Т определяют по формуле

, (2.22)

которую часто называют формулой Ньютона. Здесь 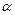- коэффициент теплоотдачи.

Величина плотности теплового потока q согласно вышеприведенной формуле будет

. (2.23)

Коэффициент теплоотдачи 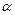зависит от скорости движения, его характера, формы и размеров тела, физических свойств (коэффициента теплопроводности, теплоемкости, плотности и вязкости), а также температуры жидкости и стенки.

Зависимость 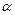от скорости равна

, (2.24)

где 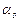- коэффициент теплоотдачи при скорости V, равной нулю, т.е. при свободной или естественной конвекции;

с и n - постоянные.

Коэффициент теплоотдачи 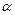характеризует собой условия теплообмена между поверхностью твердого тела и жидкостью. Численно он равен количеству тепла, переданного в единицу времени через единицу поверхности обтекаемого тела при разности температур между этой поверхностью и жидкостью в 1° С. Как видно из формулы (2.23), размерность 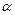в системе СИ будет - 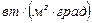, при этом значение 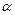меняется в весьма широких пределах.

2.3. Гипотеза сплошности

Жидкости (и газы) состоят из молекул, находящихся в состоянии хаотического движения. При крупномасштабных движениях к скорости каждой молекулы добавляется постоянный или слабоменяющийся вектор скорости. Если рассматривается объем, содержащий достаточно много молекул (в одном кубическом миллиметре воздуха при нормальных температуре (15°С) и давлении (101 кПа) содержится около 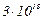молекул), движение отдельных молекул становится неразличимым; существенно лишь крупномасштабное (макроскопическое) движение.

В основе гипотезы сплошности лежит предположение о том, что в жидкостях и газах все пространство непрерывно занято веществом. Для газов, у которых длина свободного пробега молекул существенно зависит от температуры и давления, условия сплошности выражаются в том, что линейные характерные размеры области течений велики по сравнению с длиной свободного пробега молекул. Из этих же условий определяется понятие элементарного объема жидкости или газа. Линейные размеры элементарного объема должны быть достаточно большими по сравнению с длиной свободного пробега молекул газа или амплитудой колебательного движения молекул жидкости и достаточно малыми по сравнению с линейными размерами, характеризующими движение (диаметр трубы, размах крыла и др.). Следовательно, сплошность определяется не абсолютным состоянием жидкости и газа, а отношением параметров среды (длина свободного пробега для газов и амплитуда колебания молекул для жидкости) к линейным размерам, характеризующим потоки. Предполагая, что различные характеристики движения жидкости (давление, скорость и др.) меняются непрерывно со временем и по пространству (гипотеза сплошности), можно вывести уравнения, описывающие данные движения без учета индивидуального поведения молекул.

Таким образом под сплошной средой понимают непрерывное, безграничное или ограниченное множество (континуум) материальных точек с непрерывным распределением по их множеству вещественных, кинематических, динамических и других физических характеристик, обусловленных разнообразными как «внешними», так и «внутренними» движениями материи, включая сюда и взаимодействие среды с внешними и внутренними полями.

Модель сплошной среды отличается от дискретной системы материальных точек тем, что вместо физических величин, сосредоточенных в отдельных ее точках, приходится иметь дело с непрерывными распределениями этих величин в пространстве - скалярными, векторными и тензорными полями. Так, распределение массы в сплошной среде определяется заданием в каждой ее точке плотности среды, объемное силовое действие - плотностью распределения объемных сил, а действие поверхностных сил - напряжениями, определяемыми отношением главного вектора поверхностных сил, приложенных к ориентированной в пространстве бесконечно малой площадке, к величине этой площадки. Характеристикой внутреннего напряженного состояния среды в данной точке служит тензор напряжений, знание которого позволяет определять напряжения, приложенные к любой произвольно ориентированной площадке. Перенос тепла или вещества задается соответствующими им векторами потоков.

В кинематике сплошных сред, наряду с принятыми в кинематике дискретной системы точек понятиями перемещений, скоростей и ускорений, появляется характерное для сплошной среды представление о бесконечно малой деформации среды, определяемой тензором деформаций. Если рассматривается непрерывное движение текучей среды, то основное значение приобретает тензор скоростей деформаций, равный отношению тензора бесконечно малых деформаций к бесконечно малому промежутку времени, в течение которого деформация осуществилась.

При рассмотрении частных классов задач обычно приходится приписывать модели сплошной среды дополнительные макроскопические характеристики, определяющие ее индивидуальные материальные свойства, обусловленные действительными микроскопическими свойствами: молекулярной структурой и «скрытыми», движениями материи. В механике сплошных сред эти характеристики вводятся феноменологически, в форме заданных наперед констант или количественных закономерностей. Среди таких характеристик выделим, прежде всего, отражающие вещественные свойства среды при ее равновесном состоянии: молекулярный вес и плотность распределения массы, концентрацию примесей в многокомпонентных и многофазных смесях жидкостей, газов и твердых частиц, затем температуру и теплоемкость среды, электропроводность, магнитную проницаемость и другие физические свойства.

При наличии пространственной неоднородности в распределении физических характеристик, возникают процессы переноса количества движения, тепла, примесей, электрических зарядов и др. При сравнительно малых градиентах этих величин количество переносимой субстанции принимается пропорциональным ее градиенту, а коэффициенты пропорциональности в этих линейных законах (Ньютона - Стокса, Фурье, Фика и др.) называемые коэффициентами переноса, задаются также феноменологически в виде констант или функций от динамических и термодинамических характеристик механического и других форм движений.

Модель сплошной среды, заключающая в себе достаточное число расширяющих сферу ее применений дополнительных макроскопически выраженных свойств, широко принята как вполне удовлетворительный метод изучения движения жидкостей и газов в самых различных физических условиях. Эта модель представляет собой результат статистического осреднения скрытой молекулярной структуры среды и совершаемых внутри нее тепловых и других форм движений материи и взаимодействий между молекулами вещества. Как всякое осреднение, эта модель не может дать полной информации о происходящих на молекулярном и еще более глубоких физических уровнях микроскопических движениях материи, проявляющихся в обедненной форме макроскопической модели в виде тех или иных ее свойств.

2.4. Два режима движения жидкостей и газов

Опыты показывают, что возможны два режима или два вида течения жидкостей и газов в трубах: ламинарный и турбулентный. Указанные течения жидкости можно наблюдать на приборе, представленном на рис. 2.5.

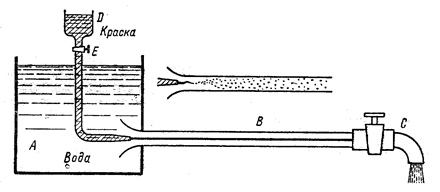
Рис. 2.5. Схема прибора для демонстрации режимов течения

Он состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором той или иной краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В. Если несколько приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Пьезометр или трубка Пито, присоединенные к трубе, показывают неизменность давления и скорости по времени, отсутствие колебаний (пульсации). Это так называемое ламинарное (слоистое) течение. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размываться и перемешиваться с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито показывают непрерывные пульсации давления и скоростей в потоке воды. Течение становится, как его принято называть, турбулентным (см. рис. 2.4, вверху). Если уменьшить скорость потока, то восстановится ламинарное течение.

Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скоростей и давления. При таком течении все линии тока вполне определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т.е. прямолинейно; отсутствуют поперечные перемещения жидкости. Ламинарное течение является вполне упорядоченным и при постоянном напоре строго установившимся течением (хотя в общем случае может быть и неустановившимся). Однако его нельзя считать безвихревым, так как в нем хотя и нет видимых вихрей, но одновременно с поступательным движением имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров с некоторыми угловыми скоростями.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Движение отдельных частиц оказывается подобным хаотическому, беспорядочному движению молекул газа. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные к оси русла составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объемов жидкости. Этим и объясняются пульсации скоростей и давления.

Режим течения данной жидкости в данной трубе изменяется примерно при определенной средней по сечению скорости течения , которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости n и обратно пропорционально диаметру d трубы, т.е. . Входящий в эту формулу безразмерный коэффициент пропорциональности k одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и вязкостью 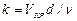. Полученное безразмерное число называют критическим числом Рейнольдса и обозначают

. (2.25)

Этот результат согласуется с теорией гидродинамического подобия, и вполне закономерно, что именно число Рейнольдса является критерием, определяющим режим течения в трубах. Как показывают опыты, для труб круглого сечения .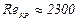

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При 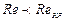течение является ламинарным, при 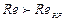- турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при 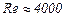, а при 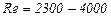имеет место переходная, критическая область. Зная скорость движения жидкости, ее вязкость и диаметр трубы, можно расчетным путем найти число Re и, сравнив его с , определить режим течения жидкости. На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно происходит в водопроводах, а также в трубах, по которым перетекают бензин, керосин, спирты, кислоты и другие маловязкие жидкости. Смена режима течения при достижении обусловлена тем, что одно течение теряет устойчивость, а другое - приобретает. При 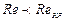ламинарное течение является вполне устойчивым: всякого рода искусственная турбулизация потока и его возмущения (сотрясения трубы, введение в поток колеблющегося тела и пр.) гасятся влиянием вязкости и ламинарное течение восстанавливается. Турбулентное течение при этом неустойчиво. При 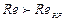, наоборот, турбулентное течение устойчиво, а ламинарное - неустойчиво. В связи с этим число , соответствующее переходу от ламинарного течения к турбулентному, может получиться несколько больше, чем для обратного перехода. В особых лабораторных условиях при полном отсутствии факторов, способствующих турбулизации потока, можно получить ламинарное течение при 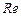, значительно превышающем . Однако в этих случаях ламинарное течение оказывается настолько неустойчивым, что достаточно небольшого возмущения (толчка), чтобы оно перешло в турбулентное. На практике обычно имеются условия, способствующие турбулизации, - вибрация труб, местные гидравлические сопротивления, неравномерность (пульсация) расхода и прочее, а потому указанное обстоятельство имеет в гидравлике скорее принципиальное, чем практическое, значение.

Дата добавления: 2014-01-06