Статистичне опрацювання експериментальних даних

Принципи кількісного аналізу, його значення та перспективи розвитку. Класифікація методів: хімічні (гравіметричний, титриметричний), фізичні та фізико-хімічні. Порівняльна оцінка методів кількісного визначення. Помилки аналітичних визначень. Метрологічні характеристики методів аналізу. Точність (правильність та відтворюваність) результатів. Статистичне опрацювання експериментальних даних.

МЕТОДІВ АНАЛІЗУ

ХАРАКТЕРИСТИКИ

КІЛЬКІСНИЙ АНАЛІЗ. МЕТРОЛОГІЧНІ

КОНСПЕКТ ЛЕКЦІЙ

з дисципліни

«АНАЛІТИЧНА ХІМІЯ ТА ІНСТРУМЕНТАЛЬНІ МЕТОДИ АНАЛІЗУ»

Розділ ІІ

«КІЛЬКІСНИЙ АНАЛІЗ. ХІМІЧНІ МЕТОДИ КІЛЬКІСНОГО АНАЛІЗУ»

для студентів напрямів:

6.051401 „Біотехнологія»,

6.051301 “Хімічна технологія»

денної та заочної форм навчання

Затверджено редакційно-видавничою секцією науково-методичної ради ДДТУ „___”_________2011 р., протокол № ___

Дніпродзержинськ

Розповсюдження і тиражування без офіційного дозволу Дніпродзержинського державного технічного університету заборонено.

Конспект лекцій з дисципліни «Аналітична хімія та інструментальні методи аналізу» розділ ІІ «Кількісний аналіз. Хімічні методи кількісного аналізу» для студентів напрямів: 6.051401 „Біотехнологія», 6.051301 “Хімічна технологія» денної та заочної форм навчання / Укладач. О.І., Полянчиков. - Дніпродзержинськ: ДДТУ, 2011. – 48 с.

Укладач: кандидат технічних наук, доцент Полянчиков О.І.

Відповідальний за випуск: завідувач кафедри ПБЗХ,

доктор хімічних наук, професор Кузнецов О.О.

Рецензент: доктор хімічних наук, професор Кузнецов О.О.

Затверджено на засіданні кафедри ПБЗХ

(протокол № ____від__________2011 р.)

Коротка анотація видання. Конспект лекцій відповідає робочій програмі дисципліни «Аналітична хімія та інструментальні методи аналізу», яка вивчається студентами напрямів: 6.051401 „Біотехнологія», 6.051302 “Хімічна технологія та інженерія» денної та заочної форм навчання. Розглянуті основні хімічні методи кількісного аналізу, їх сутність, теоретичні основи, розрахункові формули

ЗМІСТ

2.1 КІЛЬКІСНИЙ АНАЛІЗ. МЕТРОЛОГІЧНІ ХАРАКТЕРИСТИКИ

МЕТОДІВ АНАЛІЗУ 4

2.2 ГРАВІМЕТРІЯ(ВАГОВИЙ АНАЛІЗ) 10

2.3 ТИТРИМЕТРІЯ(ОБ’ЄМНИЙ АНАЛІЗ) 15

2.4 КИСЛОТНО-ОСНОВНЕ ТИТРУВАННЯ20

2.5С ПРИНЦИПИ РОЗРАХУНКУ КРИВИХ ТИТРУВАННЯ 24

2.6 ОКИСНО-ВІДНОВНЕ ТИТРУВАННЯ 31

2.7С МЕТОДИ РЕДОКСИМЕТРІЇ 36

2.8С МЕТОДИ ОСАДЖЕННЯ В ТИТРИМЕТРІЇ 41

2.9 КОМПЛЕКСОНОМЕТРІЯ 43

ЛІТЕРАТУРА 47

Кількісний аналіз забезпечує кількісне визначення компонентів, які були знайдені в результаті якісного аналізу. Він дає можливість визначати молекулярний та елементний склад речовини, що аналізується, або вміст окремих компонентів. Кількісний аналіз може бути повним, коли визначається вміст усіх елементів, іонів і сполук. Іноді визначають лише окремі елементи чи іони, або форму, у якій даний елемент знаходиться в аналізуємій речовині (наприклад нітроген у нітратній, нітрітній, ціанідній і інших формах). В залежності від задачі аналізу може визначатися вміст основної речовини (наприклад вміст СаО у вапняку), або вміст домішок. Велике значення приділяють вмісту мікро домішок, особливо при аналізі навколишнього середовища. Таким чином кількісний аналіз можна характеризувати як сукупність методів, які дозволяють з необхідною точністю визначати кількісний склад окремих складових, речовини, що аналізується, або кількісний вміст мікро домішок.

За вимірюваною властивістю речовини методи кількісного аналізу класифікують на хімічні, фізичні і фізико-хімічні.

Хімічні методи аналізу базуються на хімічних реакціях, при проведенні яких виникає аналітичний сигнал (маса осаду - ваговий аналіз, об’єм реактиву – об’ємний аналіз). До хімічних методів кількісного аналізу відносять: ваговий аналіз(гравіметрія), об’ємний аналіз(волюмометрія, титриметрія) і об’ємний газовий аналіз. Останній в сучасній практиці хімічного аналізу майже не застосовується. Порівняння вагового і титриметричного аналізів наведено у таблиці 2.1. Не дивлячись на розвиток інструментальних методів хімічні методи не втратили свого значення, особливо при арбітражному аналізі.

Таблиця 2.1 - Порівняння вагового і титриметричного методів

Показники	Ваговий аналіз	Титриметричний аналіз
1.Концентрація реактивів	Приблизна	Точно визначена
2.Кількість реактиву	Надлишок	Точно визначена
3.Момент еквівалентності	Не має значення	Фіксується
4.Тривалість аналізу	До 1-2 діб(багато часу на осадження, старіння осаду і фільтрацію)	Порівняно незначна

Фізичні методи засновані на існуванні залежності між вмістом речовини, що аналізують і фізичними властивостями проби (вимірювання інтенсивності випромінювання, електричної провідності та інше).

В фізико-хімічних методах проводять хімічну реакцію, за ходом якої стежать фізичними методами.

Традиційно фізичні і фізико-хімічні методи об’єднують під загальною назвою інструментальні методи аналізу (фотометрія, потенціометрія, емісійний спектральний аналіз, люмінесцентний та інші).

Хімічні і інструментальні методи мають свої позитивні властивості і недоліки. Хімічні методи точні (відносна похибка 0,5-1,0%), дешеві, не потребують використання спеціального обладнання. Але вони не експресні (довготривалі), трудоємкі, потребують багато часу на підготовку проби для аналізу і характеризуються малою чутливістю. При їх використанні часто потребується концентрирування і маскування. Інструментальні методи мають велику чутливість(низька межа виявлення), експресні (іноді 2-3 хвилини), можуть використовуватися іноді без спеціальної підготовки проби, але потребують спеціального обладнання, висококваліфікованого персоналу і мають порівняно низьку точність (до 50% в залежності від методу і вмісту аналізуємої речовини).

Як би прискіпливо ми не виконували аналітичні вимірювання їх результат завжди містить помилку. Залежно від форми вираження розрізняють абсолютну і відносну похибки вимірювань. Абсолютна похибка визначається в однакових одиницях вимірювальної величини і розраховується за формулою:

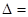Х_і – Х_іст.,

де Х_і – результат і-того вимірювання;

Х_іст. – істинне(дійсне) значення вимірювальної величини.

Відносна похибка це відношення абсолютної похибки до істинного(дійсного) значення вимірювальної величини, виражається частіше у %, і розраховується за формулою:

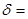
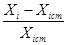*100%.

Відносна похибка засобів вимірювальної техніки, яка віднесена до діапазону вимірювання, зветься класом точності.

Залежно від характеру виникнення похибки класифікують на систематичні, випадкові і грубі.

Систематичні помилки постійні у всіх вимірах однакової величини, або змінюються по постійно діючому закону і вони є слідством дії постійної причини. Ці похибки пов’язані з інструментом, методикою вимірювання, похибками стандартних зразків.

Випадкові помилки у процесі вимірювання змінюються випадково і є дією випадкових факторів.

Результат виміру, що містить грубу помилку, істотно відрізняється від результатів повторних вимірів однакової величини, а сама похибка значно перевищує очікувану для даного ряду вимірів.

Результатам вимірювання можна дати метрологічну характеристику: точність, правильність, збіжність. Метрологія – наука об вимірюваннях, засобах досягнення їх єдності і методах забезпечення необхідної точності.

Правильність характеризує наближеність до нулю систематичної похибки.

Збіжність відображає близькість результатів паралельних вимірювань, виконаних в однакових умовах і характеризує випадкову похибку.

Відтворюваність відображає близькість результатів паралельних вимірювань, виконаних у різних умовах і характеризує випадкову похибку.

Точність – це близькість к нулю систематичної і випадкової помилок. Точність часто характеризують відносною помилкою(%).

Чутливість – відношення змінення аналітичного сигналу на виході до сигналу на вході, який визвав це змінення:

S=.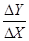

Границя виявлення – найменший вміст визначаємого компоненту, який можливо виявити за даною методикою с заданою довірливою вірогідністю. Кількісно:

,

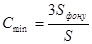де S_фону – стандартне відхилення аналітичного сигналу фону.

S - чутливість

Діапазон визначаємих концентрацій – область значень визначаємого вмісту, яка передбачена даною методикою і обмежена нижньою і верхньою границями.

На рис. 2.1 графічно показані результати паралельних вимірів за чотирма методиками і наведена кожному методу метрологічна характеристика за відхиленням середнього арифметичного від істинного значення.

1.Результати збіжні, але не правильні, 2-Результати не збіжні, але правильні, 3-Результати і не правильні і не збіжні, 4-Результати точні.

Рис. 2.1 - Метрологічні характеристики хімічного аналізу

Якщо результати вимірів містять тільки систематичну похибку, то вона стала у всіх вимірюваннях. Виявити систематичну помилку можливо таким чином:

1.Змінювати розмір проби.

2.Метод «введено-знайдено». До проби додається точно відома кількість аналізуємого компоненту, яка повинна визначатися з заданою точністю.

3.Виконувати аналіз стандартного зразку, який готують з речовини, склад і якість якої надійно встановлені і офіціально затверджені. Склад і якість стандартного зразку повинні бути близькі до аналізуємої проби. Врахувати систематичну помилку можливо, якщо ввести поправку, яка по знаку протилежна похибці, а за величиною дорівнює їй.

Врахувати випадкову помилку значно складніше, тому що вона в кожному вимірюванні не однакова і змінюється як за величиною, так і за знаком. Але використовуючи методи математичної статистики і теорії імовірності можливо оцінити вплив випадкових помилок на результати аналізу. Для цього виконують декілька аналізів однієї проби в одних і тих же умовах, так звані паралельні вимірювання.

Результати хімічного аналізу частіш за все підпорядковуються гаусовскому(нормальному) закону розподілу випадкової помилки, який в математичній формі має вигляд:

,

де 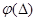- густина розподілу імовірності;

- генеральна дисперсія;

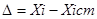- абсолютна помилка.

Основними числовими параметрами нормального закону розподілу є істинне значення вимірюваної величини(математичне очікування) і генеральна дисперсія.

Щоб отримати істинне значення(математичне очікування) треба виконати безліч паралельних вимірювань і отримати так звану генеральну сукупність всі результати, які можна було б отримати при аналізі одного і того ж об’єкту різними методами на різних приборах різними аналітиками. Однак дослідник має змогу виконати «вибірку» - реальну кількість вимірів, зазвичай 5-15, і на їх основі розрахувати вибіркові значення математичного очікування і дисперсії.

Вибірковим значенням математичного очікування є середнє арифметичне значення результатів, яке розраховується за формулою:

,

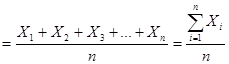де Х₁, Х₂, Х₃, …Х_n – результати паралельних вимірювань;

i = 1, 2, 3, … n,

n – число паралельних вимірювань,

– середнє арифметичне значення вимірюваної величини.

Вибіркове значенням дисперсії:

S²=.

Cтандартне відхилен­ня окремого вимірювання розраховують за формулою:

,

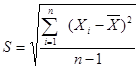де S – стандартне відхилення окремого вимірювання.

Передбачити випадкову помилку у кожному вимірюванні неможливо, але з якоюсь вірогідністю Р можливо визначити інтервал, у який попадає результат окремого вимірювання. Цей інтервал зветься довірчим інтервалом 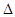, а вірогідність Р – довірчою вірогідністю. Довірчий інтервал окремого вимірювання визначають за формулою:

,

де t(P)- так званий t – розподіл – розподіл Стьюдента(таблиця 2.2.).

Середньо арифметична величина є випадковою і вона теж підпорядковується нормальному закону розподілу. Стандартне відхилен­ня середньо арифметичного розраховують за формулою:

.

Таблиця 2.2 - Залежність t- розподілу від n для різних значень ймовірностей Р

n	Р=0,90	Р=0,95	Р=0,99
	6,31	12,7	63,66
	2,92	4,30	9,93
	2,35	3,18	5,84
	2,13	2,78	4,60
	2,02	2,57	4,03
	1,94	2,45	3,71
	1,90	2,37	3,50
	1,83	2,26	3,25.

Довірчий інтервал середньо арифметичного визначають за формулою:

.

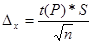І тоді результати аналізу виражають таким чином. Говорять, що з довірчою вірогідністю Р результат окремого вимірювання попадає у довірчий інтервал:

- + ,

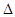
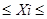
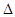а істинне значення вимірюваної величини з такою ж вірогідність знаходиться в довірчому інтервалі:

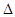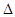- _х- _х.

Як правило, похибку результату вимірів оцінюють при довірчій імовірно­сті Р =0,95 (95% - на імо­вірність). Вибір значення Р обґрунтовується ступенем відповідальності ре­зультату вимірів. Якщо похибка у вимірах може привести до аварій, масштабних за­бруднень, екологічних катастроф, значення Р збільшують. При визначенні значення певного компоненту раціонально викону­вати не більше 3-4 паралельних аналізів, тому що далі збільшення n мало впливає на величину t(P), тобто на точність аналізу.

Важливо визначити статистичну достовірність середнього значення , тобто переконатися в тому, що при виконанні паралельних аналізів не було допущено випадкової грубої помилки. При невеликих значеннях n випадкові грубі помилки знаходять за допомогою розмаху варіювання. Для цього роз­раховують відношення:

, ,

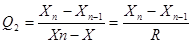де X₁, Хn – значення, які викликають сумнів,

X₂, Х_n-1 – сусідні значення;

R – розмах варію­вання.

Розраховані величини Q порівнюють із значеннями Q (Р, п), наведе­ними в таблиці 2.3. Якщо Q>Q(P, n), то це вказує на наявність грубої помил­ки. В такому разі відповід н ий результат одиночного вимірювання X відкида­ють і повторюють розрахунки X, S та 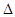для значення n-1.

Таблиця 2.3 - Числові значення Q (Р,n)

n	P=0,90	P=0,95	P=0,99
	0,89	0,94	0,99
	0,68	0,77	0,89
	0,56	0,64	0,76
	0,48	0,56	0,70
	0,43	0,51	0,64
	0,40	0,48	0,58

Контрольні питання до теми 2.1

2.1.Принципи кількісного аналізу, його значення, перспективи розвитку.

2.2.Помилки абсолютні, відносні, систематичні, випадкові.

2.3.Метрологічні характеристики результатів вимірювання.

2.4.Як можливо виявити і врахувати систематичну помилку?

2.5.Гаусовський закон розподілу випадкових помилок.

2.6.Як розраховується вибіркове значення математичного очікування?

2.7.Як розраховується вибіркове значення дисперсії?

2.8.Як розраховується стандартне відхилен­ня окремого вимірювання?

2.9.Як розраховується стандартне відхилен­ня середньо арифметичного?

2.10.Як виявити грубу помилку у ряді вимірювань?

2.2 ГРАВІМЕТРІЯ(ВАГОВИЙ АНАЛІЗ)

Дата добавления: 2014-01-06