Рух частинки поблизу поверхні Землі, наближене рівняння

У земних умовах часто розглядається рух частинок або тіл відносно систем координат, пов’язаних із Землею. Але Земля не є інерціальною системою відліку через те, що вона рухається відносно Сонця нерівномірно і непрямолінійно, і обертається навколо власної осі. Із значно більшою точністю вважають інерціальяною систему відліку, пов’язану із центром Сонця, а осі якої напрямлені на „нерухомі” зірки. Позначимо останню інерціальну систему . 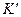Неінерціальну -систему жорстко зв’яжемо з Землею так, щоб початок її знаходився в центрі Землі. Позначимо через радіус-вектор центра Землі відносно центра Сонця, а через 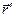– радіус-вектор частинки відносно центра Землі. З цими позначеннями рівняння руху частинки має вигляд:

В системі 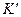на частинку крім певної сили , що залежить від конкретних умов (наприклад, сила тертя), завжди діють сили тяжіння Землі та Сонця . Тому в рівнянні

,

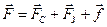
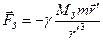
Рівняння можна спростити, якщо скористатись деякими наближеннями. Покажемо, що 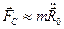. Врахуємо, що доцентрова сила, яка діє на Землю з боку Сонця, має вигляд

.

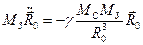Визначаючи звідси 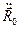, маємо

,

оскільки , якщо частинка рухається поблизу поверхні Землі.

Крім того, можна знехтувати нерівномірністю обертання Землі навколо своєї осі, поклавши . Далі, вважатимемо, що при русі частинки її відстань до поверхні Землі значно менша за радіус Землі 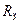. В цьому разі рівняння руху набуває вигляду

.

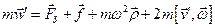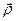Тут ми записали відцентрову силу інерції у вигляді , де модуль вектора – найкоротша відстань частинки до осі обертання, а направлений вектор 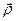від осі (рис.27). Перепишемо силу тяжіння Землі у вигляді

,

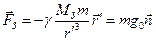де стала 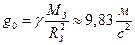, – одиничний вектор, напрямлений до центра Землі (рис.27).

Нехай частинка (тіло) не рухається відносно Землі , тоді . Оскільки тіло не рухається, то . Тоді з рівняння одержуємо

.

В даному випадку – це сила, що діє на тіло масою 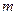з боку опори чи підвісу. Позначимо праву частину останнього рівняння величиною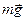

.

Величина вектора 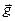називається прискоренням вільного падіння.

Сила 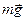, як бачимо, складається із сили всесвітнього тяжіння між частинкою і Землею та відцентрової сили, направленої перпендикулярно до осі обертання (рис.27). Як видно з малюнка, сила 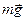(сила тяжіння) направлена не на центр Землі, а величина її залежить від широти місця.

Щоб знайти залежність сили тяжіння від широти місця 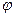застосуємо теорему косинусів до силового трикутника, побудованого на основі векторного співвідношення.

.

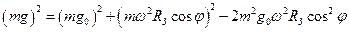Тут ми врахували вираз 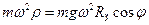для відцентрової сили. Нехтуючи другим членом, малим порівняно з іншими доданками, в правій частині останнього рівняння, одержимо

,

звідки

.

Підставляючи величини 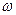і 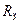для Землі отримаємо

.

Проте завдяки тому, що Земля не є точною сферою, а сплюснута біля полюсів, то залежність прискорення вільного падіння від широти сильніша і виражається такою, отриманою експериментально, формулою:

.

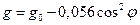Щоб знайти кут між напрямом 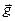і напрямом до центра Землі, застосуємо до силового трикутника теорему синусів (рис.27)

,

звідки

.

Напрям вертикалі буде співпадати з напрямом на центр Землі 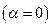на екваторі 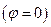і на полюсі . Найбільше відхилення, яке складає 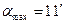спостерігається на широті .

З введенням сили тяжіння 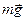, рівняння руху частинки в загальному випадку, коли 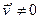, набуває такого вигляду

.

При невеликих швидкостях рухів можна навіть знехтувати останнім доданком в цьому рівнянні.

Але в деяких випадках при русі частинки поблизу поверхні Землі виникають також динамічні ефекти, пов’язані з силою Коріоліса. Розглянемо кілька прикладів таких ефектів.

Дата добавления: 2014-01-06