Величини (імпульсу, моменту імпульсу та кінетичної енергії), які можуть зберігатися в процесі руху

Розглянемо ізольовану частинку, тобто таку, на яку ніякі сили не діють: 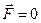, 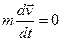. Звідси випливає, що швидкість 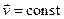. Оскільки маса частинки , то для ізольованої частинки величина .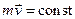

1.Вектор 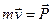називається імпульсом частинки. Отже, ізольована частинка повинна рухатися прямолінійно і рівномірно.

2.Очевидно, для ізольованої частинки зберігатиметься і скалярний добуток 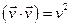, тоді буде зберігатися і величина 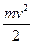. Вираз 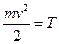називається кінетичною енергією частинки.

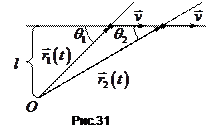3.Радіус-вектор 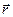частинки залежить від часу, тобто 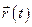змінюється. Але зберігається векторний добуток 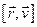(рис.31), отже, і велична 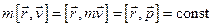. Дійсно, з рис.31, на якому показані положення частинки в два моменти часу, видно, що і напрям вектора 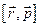залишається сталим, і його величина 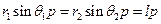. Вектор 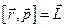називається моментом імпульсу частинки. Слід зауважити, що момент імпульсу залежить від вибору точки, відносно якої він визначається.

З’ясуємо тепер умови зміни імпульсу, моменту імпульсу та енергії частинки.

1.Запишемо похідну по часу від імпульсу, яка згідно закону Ньютона дорівнює силі

.

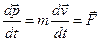Отже, причиною зміни імпульсу є сила.

2.Візьмемо похідну по часу від моменту імпульсу

.

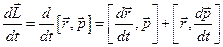Перший доданок в правій частині рівняння дорівнює нулю внаслідок колінеарності векторів 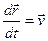і 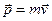; а другий доданок дорівнює величині, яка називається моментом сил 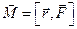. Як бачимо, умовою зміни моменту імпульсу частинки є момент сили

.

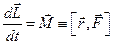Наведемо приклад. Припустимо, що сумарний момент сил відносно початку системи координат рівний нулю, тоді згідно з момент імпульсу зберігається, тобто 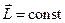. Такий момент утворює, наприклад, центральна сила, закон якої визначається виразом 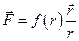. Дійсно, 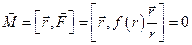. Тоді 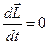, а тому .

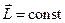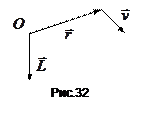Із означення векторного добутку 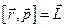випливає: 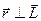, , 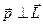а оскільки 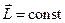, то вектори 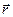і 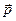лежать в одній площині, тобто траєкторія частинки під дією центральної сили є плоска фігура (рис.32).

3.Розглянемо тепер як змінюється кінетична енергія частинки 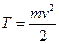. Продиференціювавши цей вираз по часу одержимо

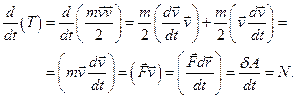
Звернемо увагу на те, що швидкість зміни кінетичної енергії дорівнює потужності, яка визначається роботою сили за одиницю часу.

Тут 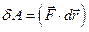– величина, яка називається елементарною механічною роботою. Отже, з видно, що приріст кінетичної енергії 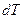частинки дорівнює елементарній роботі сили:

.

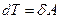Якщо на частинку в процесі руху діють декілька сил, результуюча яких 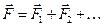, то робота результуючої сили дорівнює сумі робот всіх сил, якими виконується робота

.

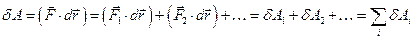Дата добавления: 2014-01-06