
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рух тіла змінної маси
|
|
|
|
Існує багато таких прикладів, коли маса тіла неперервно змінюється в процесі руху (космічний човен, літак, платформа, що навантажується на ходу і інші).
Наша задача: знайти рівняння руху такого тіла.
Розглянемо рух тіла (матеріальної точки), здатного виштовхувати частину своєі маси з певною швидкістю або приєднувати будь-яку масу (наприклад, втягувати в себе повітря). Щоб записати рівняння руху цього тіла, скористаємось загальним законом механіки – законом зміни імпульсу з часом:
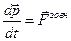 .
.
 Обчислимо зміну імпульсу, враховуючи імпульс, що вноситься і виноситься масами, які приєднуються і відокремлюються.
Обчислимо зміну імпульсу, враховуючи імпульс, що вноситься і виноситься масами, які приєднуються і відокремлюються.
Нехай в момент часу  тіло мало масу
тіло мало масу 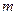 , швидкість
, швидкість 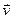 ; маса частинок, що від’єдналася,
; маса частинок, що від’єдналася,  і її швидкість
і її швидкість 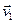 ; маса частинок, що приєднається,
; маса частинок, що приєднається, 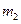 і її швидкість
і її швидкість 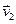 (рис.35). Згідно з означенням імпульсу, маємо
(рис.35). Згідно з означенням імпульсу, маємо
 .
.
У момент часу  тіло змінило свою масу за рахунок мас, що приєднуються і відокремлюються, і тепер його маса дорівнює
тіло змінило свою масу за рахунок мас, що приєднуються і відокремлюються, і тепер його маса дорівнює  , а швидкість
, а швидкість  ; маса частинок, що відокремилися,
; маса частинок, що відокремилися,  , а швидкість
, а швидкість 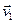 ; аналогічно, маса частинок, які приєднуються,
; аналогічно, маса частинок, які приєднуються, 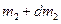 , а їх швидкість
, а їх швидкість 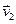 (вважаємо, що швидкість мас, які приєднуються і відокремлюються, залишається сталою). Очевидно, і мпульс у момент часу
(вважаємо, що швидкість мас, які приєднуються і відокремлюються, залишається сталою). Очевидно, і мпульс у момент часу  буде
буде
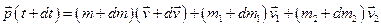 .
.
Оскільки повна маса зберігається, то
 .
.
Обчислимо похідну
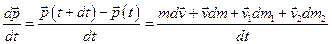
тут ми знехтували 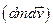 – величиною другого порядку малості. Враховуючи співвідношення, запишемо у вигляді
– величиною другого порядку малості. Враховуючи співвідношення, запишемо у вигляді
 .
.
Вектори 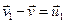 і
і 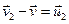 це швидкості (відносні), з якими маси, що відокремлюються від тіла і приєднуються до нього, рухаються відносно самого тіла. Підставивши у формулу відносні швидкості, перепишемо її у вигляді:
це швидкості (відносні), з якими маси, що відокремлюються від тіла і приєднуються до нього, рухаються відносно самого тіла. Підставивши у формулу відносні швидкості, перепишемо її у вигляді:
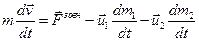 .
.
Рівняння називається рівнянням Мещерського, а два останні доданки в правій його частині є реактивними силами.
Розглянемо випадок реактивного руху (в космічному просторі). При реактивному русі тіло (ракета) рухається за рахунок зменшення своєї маси, при цьому 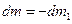 ,
, 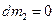 і рівняння набуває вигляду
і рівняння набуває вигляду
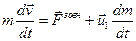 .
.
Похідна  , оскільки маса тіла з часом зменшується. Звідси випливає, що ракета буде прискорювати рух, тобто
, оскільки маса тіла з часом зменшується. Звідси випливає, що ракета буде прискорювати рух, тобто 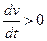 , якщо
, якщо 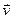 і
і 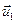 мають протилежний напрям, оскільки в цьому разі проекція реактивної сили в рівнянні на напрям
мають протилежний напрям, оскільки в цьому разі проекція реактивної сили в рівнянні на напрям 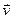 додатня.
додатня.
Другим важливим випадком руху, що описується рівнянням, є повітряно-реактивний рух. При цьому маса тіла не змінюється, тобто 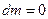 ,
, 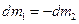 і рівняння набуває вигляду
і рівняння набуває вигляду
 .
.
У формулі похідна  , а
, а 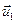 і
і  напрямлені протилежно
напрямлені протилежно 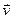 , тому проекція цього рівняння на напрям
, тому проекція цього рівняння на напрям 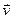 має вигляд
має вигляд
 .
.
Ясно, що рух буде з прискоренням, тобто 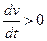 , якщо
, якщо  , тобто частинки повинні відокремлюватись з більшою відносною швидкістю, ніж їхня швидкість в момент приєднання.
, тобто частинки повинні відокремлюватись з більшою відносною швидкістю, ніж їхня швидкість в момент приєднання.
Застосування рівняння Мещерського розглянемо на найпростішому прикладі руху ракети, уперше дослідженому К.Е.Ціолковським. Приймемо припущення Ціолковського, за яким вектор відносної швидкості  відокремлюваних частинок сталий за модулем, спрямований по дотичній до траєкторії руху літального апарату і напрямлений протилежно до вектора
відокремлюваних частинок сталий за модулем, спрямований по дотичній до траєкторії руху літального апарату і напрямлений протилежно до вектора 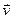 . У відсутності зовнішнього силового поля
. У відсутності зовнішнього силового поля 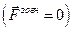 на підставі маємо проекцію рівняння руху на напрям
на підставі маємо проекцію рівняння руху на напрям 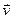
 .
.
Інтегруючи при початкових умовах:  ,
,  , дістанемо
, дістанемо
 .
.
Цю формулу вперше вивів К.Е.Ціолковський. Опубліковано її в 1903р.. Якщо 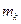 – маса літального апарата в кінці процесу згорання пального,
– маса літального апарата в кінці процесу згорання пального, 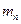 – початкова маса пального, то з рівняння отримаємо такий вираз для максимального значення швидкості ракети
– початкова маса пального, то з рівняння отримаємо такий вираз для максимального значення швидкості ракети
 .
.
З випливає, наприклад, що більш ефективним для збільшення  є не збільшення початкового запасу пального
є не збільшення початкового запасу пального 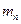 , а збільшення швидкості
, а збільшення швидкості  витікання струї газу.
витікання струї газу.
Глава 5
Закон збереження моменту імпульсу
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1837; Нарушение авторских прав?; Мы поможем в написании вашей работы!