Момент імпульсу системи частинок

Раніше для одної, наприклад, -ої частинки ми ввели поняття моменту імпульсу

,

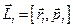тут 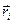– радіус-вектор, який характеризує положення -ої частинки відносно деякої точки 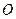вибраної системи відліку, а 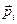– імпульс частинки (рис.36).

Диференціюванням було отримано так зване рівняння моментів, яке для -ої частинки набуває вигляду

,

де – момент сили -ої частинки, визначений відносно тієї ж самої точки .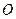

Розглянемо далі систему частинок. Введемо поняття моменту імпульсу даної системи як векторну суму моментів імпульсів її окремих частинок

,

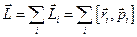де всі вектори визначені відносно однієї і тієї ж точки 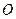вибраної системи відліку.

З’ясуємо чим визначається зміна моменту імпульсу системи. Для цього продиференціюємо по часу:

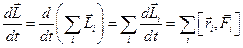
Після підстановки сили 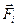, яка складається із внутрішніх і зовнішніх сил, що діють на -ту частинку

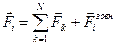
маємо

.

Другу суму в правій частині формули називають результуючим моментом зовнішніх сил:

.

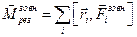Першу суму в розглянемо окремо і покажемо, що вона дорівнює нулю:

.

В другій сумі поміняємо місцями індекси суми . Від цього сума не зміниться, зміниться лише порядок розташування членів суми. В цьому легко переконатися на прикладі трьох частинок:

.

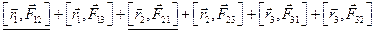Тоді матиме вигляд

,

а оскільки

,

то

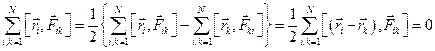оскільки вектори і колінеарні (рис.37). Отже,

,

тобто похідна по часу від вектора моменту імпульсу системи дорівнює результуючому моменту всіх зовнішніх сил, що діють на систему. Звичайно, всі моменти (сил і імпульсу) треба обчислювати відносно тієї самої точки.

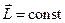Для ізольованої системи , оскільки , тоді з випливає, що , тобто момент імпульсу системи залишається сталим як за величиною, так і за напрямом. Це твердження має назву закону збереження моменту імпульсу системи частинок.

Якщо одна або дві компоненти моменту зовнішніх сил дорівнюють нулю, то зберігаються тільки відповідні компоненти вектора моменту імпульсу.

Дата добавления: 2014-01-06