Зв’язок між потенціальною енергією і силою поля

Потенціальне поле сил можна характеризувати або силою, або потенціальною енергією. При переміщенні частинки із одної точки потенціального поля в іншу робота, яку виконують сили поля, може бути представлена як зменшення потенціальної енергії частинки, тобто 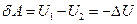. Це стосується і елементарного переміщення, для якого можна записати 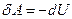, або

.

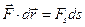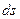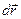З врахуванням, що , де –елементарний шлях, а – проекція вектора на переміщення , можна переписати рівняння у вигляді

,

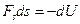де 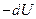є антиприріст (зменшення) потенціальної енергії на переміщенні 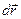. Звідси маємо

,

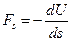тобто проекція сили на напрям переміщення 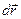, дорівнює зі знаком мінус похідній потенціальної енергії від шляху в напрямі переміщення.

Переміщення можна взяти в любому напрямі, наприклад, вздовж осі 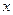, тоді отримаємо

.

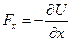Аналогічно, отримаємо і проекції , . Тоді вираз для сили має вигляд

.

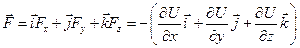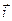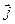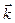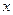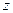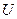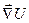Тут , , – орти відповідних осей , , . Величину, що стоїть в дужках називають градієнтом скалярної функції і позначають , або . Тут 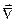(набла) – оператор, який має вигляд

.

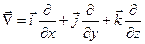Таким чином, зв’язок між силою і потенціальною енергією можна представити у такому компактному вигляді

,

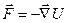тобто сила дорівнює антиградієнту потенціальної енергії. Це математичне співвідношення і є умовою потенціальності силового поля.

Для з’ясування змісту градієнта введемо поняття еквіпотенціальної поверхні – поверхні, у всіх точках якої потенціальна енергія 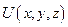має одне і те саме значення. На рис.46 показаний переріз еквіпотенціальних поверхонь площиною листа.

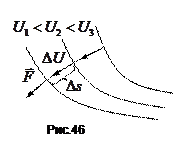З виразу випливає, що проекція сили на напрям дотичної до еквіпотенціальної поверхні дорівнює нулю. Це означає, що вектор нормальний до еквіпотенціальної поверхні в даній точці. Напрям вектора , згідно з, визначається напрямом зменшення потенціальної енергії 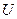, а величина 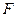дорівнює

,

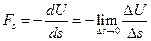де 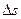– елементарний шлях вздовж нормалі до еквіпотенціальної поверхні (рис.46).

Оскільки вектор протилежний за напрямком вектору 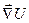, легко дійти висновку, що градієнт 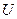– це вектор, напрямлений по нормалі до еквіпотенціальної поверхні в бік зростання потенціальної енергії.

Дата добавления: 2014-01-06