Сила затяжки болта

Сильна затяжка болта підвищує надійність роботи різьбового з’єднання, так як підвищує жорсткість стиску і при цьому суттєво понижується доля змінного (перемінного) навантаження на болт.

Щоб забезпечити необхідну силу затяжки її контролюють. Це роблять шляхом вимірювання видовження болта (шпильки), наприклад, методом тензометрії (електричні методи вимірювання механічних величин), вимірюванням кута повороту гайки або крутного моменту. Найбільш точний перший метод. Але найбільш простіший і доступний третій метод — вимірювання ключем граничного моменту або динамометричним ключем.

При цьому вважається, що розсіювання сили затяжки складає ± (25-30) %. Коефіцієнти варіації сили затяжки приблизно дорівнюють 0,02-0,09.

6.3 Напруження на болті від зовнішнього навантаження

Напруження в болті від зовнішнього навантаження визначаються з врахуванням того, що тільки 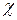-та частина навантаження передається на гвинт. Величини 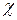називається коефіцієнтом основного навантаження і визначається

,

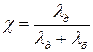де 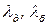— податливість деталей при достатніх силах затяжки болтів для стальних і чавунних деталей здебільшого 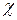=0,2-0,3.

Коефіцієнт концентрації в різьбі

Коефіцієнт концентрації в першу чергу визначається формою впадин різьби, яка може бути заокругленою або не обумовленою (СТ CЄВ 640-77).

Для відповідальних з’єднань при змінних і динамічних навантаженнях повинна використовуватися різьба з заокругленими впадинами. У такої різьби радіус 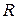кривини впадини повинен бути

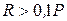, (6.1)

де Р — крок різьби.

Ефективний коефіцієнт концентрації в різьбі визначають експериментально або через теоретичний коефіцієнт концентрації напружень. Для найбільш поширеного спряження болта з гайкою, яка працює на стиснення, теоретичний коефіцієнт концентрації напружень a визначають

. (6.2)

При цьому .

Тоді середнє значення 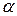і коефіцієнт варіації коефіцієнта концентрації напружень

; (6.3)

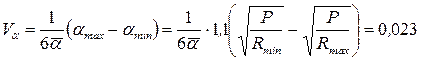. (6.4)

Для відповідальних з’єднань (авіація) , .

Ймовірний розрахунок роботоздатності, надійності з’єднання зводиться до оцінки ймовірності 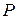(t) безвідмовної роботи з’єднання, яка в першому наближенні дорівнює

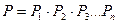, (6.5)

де — ймовірності безвідмовної роботи по основних критеріях: нерозкриттю стиску, нерухомості стиску, міцності гвинтів і т.д.

Кількість критеріїв, що враховуються визначається залежно від відповідальності з’єднання.

Рисунок 6.1 — Схема болтового з’єднання

6.5 Ймовірність безвідмовної роботи
за критерієм нерозкриття стиску 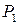(t)

Передумова ймовірності безвідмовної роботи в тому, що найменше напруження в стиску після дії зовнішнього навантаження більше нуля.

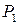Для простого випадку, коли болтове з’єднання навантаження центральною силою ймовірність (t) визначають з умови

, (6.6)

де 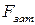— сила затяжки;

— доля зовнішнього навантаження, яке приходиться на стиск;

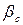— коефіцієнт, який враховує можливе послаблення затяжки внаслідок зминання стиску .

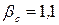Ймовірність (t) безвідмовної роботи визначають по таблиці нормального розподілу ймовірностей залежно від квантілі U_p1

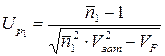, (6.7)

де — коефіцієнт запасу нерозкриття стиску по середніх навантаженнях;

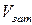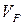, — коефіцієнти варіації сили затяжки і сили зовнішнього навантаження.

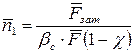. (6.8)

Сила затяжки

; (6.9)

де 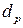— розрахунковий діаметр різьби;

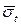— середнє значення границі текучості матеріалу болта, яке приймається по довідниках.

6.6 Ймовірність безвідмовної роботи по критерію нерухомості стиску Р ₂(t)

. (6.10)

Для визначення (t) вираховують квантіль

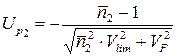, (6.11)

де 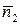— середнє значення коефіцієнта запасу нерухомості;

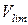— коефіцієнт варіації граничного моменту затяжки болтового з’єднання.

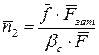; (6.12)

де 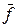— середнє значення коефіцієнта тертя між деталями, що з’єднані.

, (6.13)

де 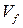— коефіцієнт варіації коефіцієнта тертя.

Величина 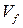приймається по довідниковій літературі залежно від матеріалу з'єднання деталей і умов роботи з’єднання.

Значення визначаємо по 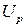по таблиці нормального нормованого розподілу ймовірностей безвідмовної роботи.

Ймовірність безвідмовної роботи 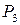(t)
по критерію статичної міцності

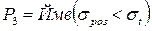, (6.14)

де — розрахункове напруження в небезпечному перерізі болта;

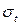— границя текучості матеріалу болта.

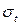і — величини випадкові.

Середнє значення розрахункового напруження в болті одиночного болтового з’єднання, навантаженого центральною відриваючою силою, визначається виразом

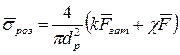, (6.15)

де 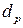— розрахунковий діаметр різьби болта;

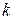— коефіцієнт, який враховує закручування болта (коли закручування при затяжці виключено 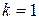, в інших випадках — ).

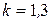Середнє квадратичне відхилення розрахункового напруження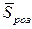

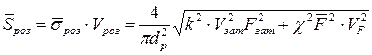, (6.16)

де — коефіцієнт варіації розрахункового напруження.

Розв’язавши рівняння відносно 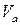, одержимо

; . (6.17)

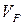Внаслідок відносної невеликої величини і відповідності і 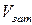в технічних розрахунках можна приймати .

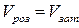Ймовірність безвідмовної роботи (t) по критерію статичної міцності знаходимо по таблиці по квантілі

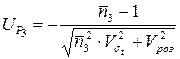, (6.18)

де — коефіцієнт запасу міцності по середніх напруженнях;

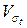— коефіцієнт варіації границі текучості матеріалу болта. В практичних розрахунках можна приймати .

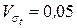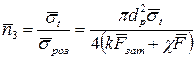. (6.19)

Ймовірність безвідмовної роботи з’єднання по критерію статичної міцності визначаємо по таблиці за .

6.8 Ймовірність безвідмовної роботи 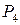(t) по критерію опору втомі

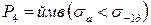, (6.20)

де — діючі напруження, приведене до симетричного циклу;

— границя витривалості болта.

Середнє діюче напруження визначаємо за формулою

, (6.21)

де — середнє (вираховуючи випадковий характер сили) значення максимального навантаження циклу;

0,5— середнє значення амплітуди навантаження;

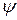— коефіцієнт чутливості матеріалу до асиметрії циклу. Для найбільш поширених матеріалів (сталь, чавун) 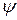=0,09-0,15;

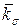— середнє значення ефективного коефіцієнта концентрації напружень. Його приймають залежно від границі міцності матеріалу 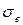, МПа:

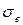
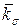
	3,0	3,9	4,8	5,7

або вираховують за формулою

, (6.22)

де — коефіцієнт чутливості матеріалу до концентрацій напружень, який дорівнює 0,5-0,6 для вуглецевих 0,7-0,8 для легованих сталей;

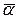— середнє значення теоретичного коефіцієнта концентрації напружень.

Коефіцієнт варіації 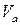напружень можна приймати рівним коефіцієнту варіації навантаження .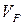

Середнє значення границі витривалості болта

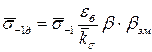, (6.23)

де 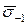— середнє значення границі витривалості гладкого взірця — приймається за довідниками;

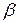— коефіцієнт стандарту. Для з’єднання стандартними болтами і гайками 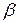=1, для з’єднань типу стяжки 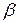=1,5-1,6;

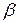_зм — коефіцієнт технологічного зміцнення, який для болтів з нарізаною різьбою дорівнює 1, а для болтів з накатаною різьбою — 1,2-1,3;

— коефіцієнт впливу абсолютних розмірів болта, який для болтів М6-М20 можна приймати рівним 1.

Коефіцієнт варіації границі витривалості болта включає коефіцієнти варіації границі витривалості деталі однієї плавки 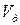, який приблизно приймається 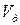=0,06-0,08, коефіцієнта границі витривалості по плавках і коефіцієнта варіації ефективного коефіцієнта концентрації напружень , який приблизно дорівнює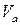

. (6.24)

Ймовірність безвідмовної роботи з’єднання по критерію опору втомі 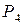(t) визначаємо залежно від квантілі нормативного нормального розподілу

; , (6.25)

де — середнє значення коефіцієнта запасу міцності по критерію опору втомі.

Ймовірність безвідмовної роботи 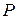з’єднання по чотирьох критеріях, розглянутих вище, буде дорівнювати

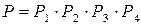. (6.26)

7 НАДІЙНІСТЬ ЗУБЧАТИХ ПЕРЕДАЧ

7.1 Розрахунок надійності зубчастих передач
за умовою опору контактній втомі

Враховуючи широке використання зубчастих передач, питання їх надійності досить актуальне. Адже, більше 30% передач в машинобудуванні зубчасті.

Розрахунок як і в попередніх розділах зводиться до співставлення по окремих критеріях розрахункових параметрів з їх граничними величинами — границею міцності, текучості, витривалості, граничних навантаження, переміщення тощо. Ймовірність безвідмовної роботи Р_н (t) за критерієм опору контактній втомі визначається як ймовірність того, що контактне напруження (розрахунковий параметр) s_н не перевищує границі контактної витривалості (граничне значення розрахункового параметра) s_{н lim}, тобто

Р_н = Ймв (s_н < s_{н lim}). (7.1)

Контактні напруження s_н, МПа, які діють в полюсі зачеплення

, (7.2)

де Z_н — коефіцієнт, який враховує форму спряжених поверхонь;

a_w — міжосьова відстань, мм;

b_w — робоча ширина вінця, мм;

и — передавальне число;

Т_1н — крутний момент на шестерні при роботі в номінальному режимі, Н×м;

к_нå — коефіцієнт навантаження.

Напруження s_н розглядається як функція випадкової величини, яка дорівнює добутку чотирьох випадкових величин:

к_нå = к_А × к_нb × к_нv × к_нa, (7.3)

де к_А — коефіцієнт зовнішнього навантаження;

к_нb — коефіцієнт розподілу навантаження по ширині вінця;

к_нv — коефіцієнт динамічного навантаження, яке виникає в зачепленні;

к_нa — коефіцієнт розподілу навантаження між зубцями.

У формулі (7.2) Т_1н та інші вважаються детермінованими величинами. Випадковий характер зовнішнього навантаження вираховуються коефіцієнтом к_А.

Коефіцієнт варіації коефіцієнта навантаження к_нå визначається залежно від випадкових незалежних величин

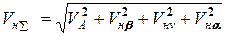, (7.4)

де V_A, V_нb, V_нv, V_нa — коефіцієнти варіації відповідних коефіцієнтів к_А , к_нb, к_нv , к_нa.

Ймовірність безвідмовної роботи за критерєм опору контактній втомі визначається за таблицями нормального розподілу ймовірностей безвідмовної роботи залежно від величини квантілі U_p, яка дорівнює

, (7.5)

— коефіцієнти запасу міцності по середніх напруженостях; 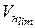— коефіцієнт варіації границі витривалості; — коефіцієнт варіації розрахункового напруження.

Коефіцієнти запасу міцності 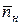дорівнює

. (7.6)

Середнє значення напруження визначається із залежності

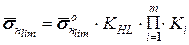, (7.7)

де 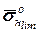— середнє значення границі витривалості базового взірця;

— коефіцієнт довговічності;

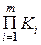— добуток т коефіцієнтів, які враховують вплив мастил, розмірів зубчастих коліс, шорсткості спряжених поверхонь, колову швидкість.

Значення К_НL і 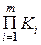приймають по стандарту 21354-75 або визначають по емпіричних формулах.

Коли відсутні надійні експериментальні дані по 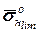, то можна користуватися емпіричними залежностями

, (7.8)

де К_р — коефіцієнт ймовірності неруйнування;

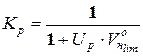, (7.9)

а, в — постійні значення, які приймаються по стандарту. Наприклад, для нормалізованих і покращених сталей а =2, в =20 (стандарт 21354-75).

— середня твердість поверхні зубця;

. (7.10)

де 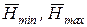— нижнє і верхнє поля допуску твердості поверхні зубця, можна приймати ;

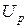— квантіль нормованого нормального розподілу ймовірності неруйнування.

У практичних розрахунках можна приймати U_p =0. По інших рекомендаціях ймовірність неруйнування приблизно оцінюють рівною 0.8-0,9, що відповідає квантілі U_p =-(0,84-1,28).

У закордонних методиках ймовірність неруйнування приймають 0,9-0,99, що відповідає U_p =-1,28¸-2,32.

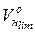— коефіцієнт варіації границі витривалості взірця. Для зубців без термічної обробки 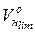=0,08-0,1 і 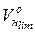=0,1-0,12 для покращаних зубців.

Значення коефіцієнта варіації границі витривалості примається дещо більшим, як для базового взірця.

. (7.11)

Враховуючи пропорційну залежність s_н від , можна приймати значення коефіцієнта варіації 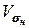контактного напруження рівним

. (7.12)

Для визначення V_Hå визначаються значення коефіцієнтів варіації V_A, V_нb, V_нv, V_нa відповідних коефіцієнтів к_А , к_нb, к_нv , к_нa.

Так як для зубчастих передач, зовнішнім навантаженням є момент, то коефіцієнт зовнішнього навантаження

, (7.13)

де 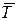— середнє значення крутного моменту, задане в зовнішньому навантаженні, Нм і відповідно

V_A = V_T, (7.14)

де V_T — коефіцієнт варіації крутного моменту.

Коефіцієнт розподілу навантаження по ширині зубця к_нb залежить від сумарної питомої жорсткості спряжених зубців, кута перекосу зубців, припрацювання зубців через неточність виготовлення і приведеної колової сили. Середнє значення цього коефіцієнта знаходиться в границях .

Допускаючи, що поле розсіювання перекривається (6) середніми квадратичними відхиленнями, одержують вираз для визначення V_нb

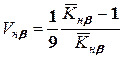. (7.15)

Значення коефіцієнта к_нv динамічного навантаження визначається трьома факторами: різницею в кроках зачеплення, часу дії динамічного навантаження і припрацюванням зубців.

Середнє значення вибирають за стандартами. Коефіцієнти варіації V_нv при твердості поверхні зубців Н >HB350

, а при твердості Н £HB350

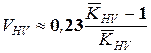. (7.16)

Коефіцієнти K_нa розподілу навантаженні між зубцями приймається за стандартами.

У практичних розрахунках на надійність коефіцієнти варіації V_нa коефіцієнта K_нa рекомендується вибирати із залежності

кнa	1-0,95	0,95-0,9	0,9-0,85	0,85-0,8	£0,8
Vнa		0,05	0,08	0,05

Коли працює одна пара зубців к_нa =0,7¸0,9.

7.2 Розрахунок надійності зубчастих передач на опір при згині

В якості розрахункового параметру приймають напруження на перехідній поверхні зубця s_F, МПа, яке визначається за формулою

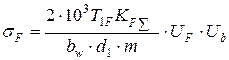, (7.18)

де Т _{1 F} — номінальний крутний момент на шестерні, Н×м;

b_w — ширина зубця, мм;

d ₁ — ділильний діаметр шестерні, мм;

т — модуль, мм;

и_F — коефіцієнт форми зубця;

и_в — коефіцієнт, який враховує нахил зубця;

К_Få — коефіцієнт навантаження.

Напруження згину s_F розглядають як випадкову величину, яка є функцією коефіцієнта навантаження К_Få. Інші параметри в формі є детерміновані, спосіб визначення яких регламентується стандартом.

Коефіцієнт навантаження К_Få, так як і в розрахунку на опір контактній втомі враховує одні і ті ж фізичні явища.

Тому структура коефіцієнта навантаження К_Få аналогічна:

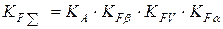, (7.19)

де К_А — коефіцієнт зовнішнього навантаження;

К_Fb — коефіцієнт розподілу навантаження по ширині зубця;

К_FV — коефіцієнт динамічного навантаження;

К_Fa — коефіцієнт розподілу навантаження між зубцями.

Між коефіцієнтами К_Нå і К_нF існує залежність, близька до пропорційної.

Тому в розрахунках значення коефіцієнта варіації V_Få коефіцієнта К_Få можна приймати рівним коефіцієнту варіації V_Нå коефіцієнта К_Нå

V_Få = V_Нå. (7.20)

Середнє значення коефіцієнта навантаження 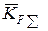приймають рівним добутку середніх значень коефіцієнтів , , , .

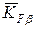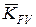Мінімальні значення коефіцієнтів К_Fb, К_FV, К_Fa приймають за стандартом.

Надійність безвідмовної роботи Р_н за критерієм опору втомі при згині визначають за таблицею нормованого нормального розподілу ймовірностей залежно від квантілі U_р

, (7.21)

де — коефіцієнт запасу міцності по середніх напруженнях;

— коефіцієнт варіації граничного напруження s_Flim;

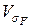— коефіцієнт варіації розрахункового напруження s_F на передній поверхні зубця.

. (7.22)

Середнє значення границі витривалості 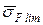визначають за формулою

, (7.23)

де 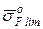— середнє значення границі витривалості зубців базового взірця — здебільшого зубчатого колеса з модулем 3 мм (рідше 5 мм);

К_Z — коефіцієнт, який враховує багатоелементність зубчастого колеса;

К_FL — коефіцієнт довговічності;

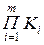— добуток корегуючих коефіцієнтів, які враховують масштабний фактор, технологію виготовлення, шорсткість поверхні.

Для нормалізованих і покращених сталей

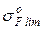=1,35Н+100, (7.24)

де Н — твердість матеріалу по Брінелю.

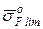Для цементованих сталей МПа. При визначенні рекомендується значення 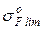множити на коефіцієнт К_р, який враховує ймовірність границі витривалості.

Його визначають так само, як і в розрахунку 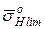тільки замість підставляємо значення коефіцієнта варіації границі витривалості, тобто

. (7.25)

приймаємо:

— для нормалізованих і покращаних зубчастих коліс – 0,08-0,1;

— для коліс з загартуванням СВЧ — 0,1-0,14;

— для азотованих коліс – 0,1-0,12.

Зубчате колесо можна розглядати як послідовну систему, яка складається з Z елементів-зубців. Руйнування колеса пов’язане з найменш міцного зубця. Це враховується тим, що в розрахункові залежності вводиться коефіцієнт К_Z.

Значення К_Z для числа зубців Z =20¸100 залежно від різних значень приймаються

	0,08	0,1	0,12	0,14
КZ	0,85¸0,80	0,80¸0,75	0,77¸0,70	0,75¸0,65

Величини коефіцієнту К_FL і добуток корегуючих коефіцієнтів приймаються за стандартом.

Коефіцієнт варіації V_Flim границі витривалості визначається

, (7.26)

де a_Z — параметр, який враховує багатоелементність зубчатого колеса і залежить від К_Z і .

	0,08	0,10	0,12	0,14
aZ	0,85¸0,80	0,80¸0,75	0,77¸0,70	0,75¸0,65
КZ	0,62¸0,54	0,65¸0,57	0,68¸0,6	0,70¸0,66

Коефіцієнт варіації 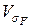розрахункового напруження s_F на перехідній поверхні зубця приймаємо

. (7.27)

Ймовірність безвідмовної роботи Р_F по критерію опору втомі при згині визначають за таблицями нормованого нормального розподілу по U_p.

Надійність зубчатих передач в комплексі

Для широкого кола зубчатих передач, у яких найбільш небезпечні втомні руйнування, ймовірність безвідмовної роботи дорівнює

, (7.28)

де Р_н і Р_F ймовірність безвідмовної роботи по критерію опору втомі при контакті і згині відповідно.

Для більш точних розрахунків ймовірність безвідмовної роботи рекомендується вираховувати за формулою (приблизно)

, (7.29)

де Р_і — ймовірність безвідмовної роботи передачі по і-тому критерію;

п — число критеріїв.

Дата добавления: 2014-01-06