Простые схемы отбора

1. Простая случайная выборка обычно применяется в тех ситуациях, когда известны характеристики генеральной совокупности. Она должна обеспечивать равный шанс попадания элементов генеральной совокупности в выборочную (простейший пример – тираж спортлото). При этом можно применить два метода отбора: случайно-бесповторный и случайно-повторный. В первом случае каждый элемент генеральной совокупности может попасть в выборку только один раз, а во втором – более одного раза.

У обоих методов есть общий недостаток: их можно успешно применять только для генеральных совокупностей, насчитывающих не более 800 – 1000 единиц. Для больших генеральных совокупностей удобнее применять метод механической выборки.

Простая случайная выборка строится с помощью таблиц случайных чисел, поэтому достаточно иметь в качестве предварительной информации о генеральной совокупности перечень или опись ее элементов. Однако, необходим перечень всех элементов генеральной совокупности. Кроме этого, применение случайной выборки возможно только при качестве однородных объектов.

2. Систематическая выборка (механическая) позволяет при небольшом объеме охватить большие генеральные совокупности. Она представляет такой вид отбора нужного количества элементов из списка элементов исходной совокупности, который осуществляется через равные интервалы (шаги). Этот интервал (шаг) определяется путем деления объема генеральной совокупности на объем выборочной.

Например, список фамилий студентов вуза включает 2000 человек, а необходимый объем выборки – 200 человек. Первый элемент выбирается случайно, допустим с помощью лотереи. Выпало число 5. Теперь определяем интервал (шаг).

Он рассчитывается по формуле:

,

где А – величина генеральной совокупности, а – величина выборочной совокупности.

Тогда,

.

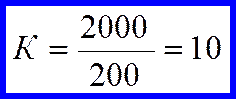Это означает, что из списка должна быть отобрана каждая десятая единица. Приступая к систематической выборке, находим первое число 5, затем 15, 25, 35 и т.д. Таким образом, набираем фамилии 200 студентов.

В качестве недостатка данного вида выборки можно отметить возможное смещение в случае совпадения интервала отбора с невыявленной переодичностью распределения признака в генеральной совокупности.

3. Серийная (гнездовая) выборка – это такой вид выборки, при котором единицами случайного отбора являются определенные серии, гнезда (семьи, коллективы, жилые кварталы и т.п.). Преимущество этого вида заключается в том, что гораздо проще определить перечень серий, гнезд, чем единиц отбора, тем не менее, здесь, возможно занижение разброса (дисперсии) изучаемого признака в силу определенного сходства единиц в гнездах.

Суть метода серийной выборки заключается в том, что генеральная совокупность разбивается на однородные части (серии) по заданному признаку, и отбор респондентов осуществляется из каждой серии отдельно. При этом число респондентов, отбираемых из серии, пропорционально общему числу элементов в ней.

Допустим, что генеральная совокупность в 2000 студентов включает в себя 500 отличников, 1200 хорошистов и 300 троечников. Выборочная совокупность планируется в 200 студентов. Количество респондентов из каждой серии определяется по следующей формуле:

,

где х – число серий, выделенных в генеральной совокупности,

А_х – число единиц в серии,

А – величина генеральной совокупности,

а – величина выборочной совокупности.

Следовательно, из каждой серии подлежит отбору и опросу:

= 50 студентов;

= 120 студентов;

= 30 студентов.

Общая величина выборочной совокупности равна:

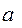= = 50 + 120 + 30 = 200 студентов.

4. Метод гнездовой выборки предполагает отбор в качестве единиц исследования не отдельных респондентов, а групп или коллективов с последующим сплошным опросом в отобранных группах.

Например, в институте 100 групп студентов, в каждой из которых занимается по 20 человек. На основе случайной выборки может быть отобрано 10 групп. В этом случае опросу подлежит 200 человек.

Необходимо только учитывать, что гнездовая выборка представительна (репрезентативна) при максимальной степени схожести состава групп

Дата добавления: 2014-01-07