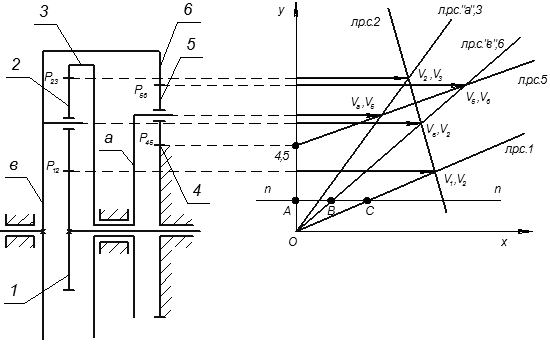
Графическое определение передаточного отношения. Построение картины скоростей этого механизма нельзя начинать с его свободного звена, т.е

Построение картины скоростей этого механизма нельзя начинать с его свободного звена, т.е. с колеса 1. Во избежание ошибок начинаем построение с замыкающей цепи.

Выбираем прямоугольную систему координат с началом координат на центральной оси механизма и задаёмся окружной скоростью точки водила «а», лежащей на оси сателлита 5. Эту скорость изображаем отрезком , проведенным горизонтально на уровне оси блока сателлитов от вертикальной оси 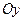. Так как скорость точки водила «а» на центральной оси равна нулю, то, соединив конец отрезка с началом координат, получаем линию распределения скоростей водила «а». Эта линия будет и линией распределения скоростей колеса 3, т.к. водило «а» и колесо 3 соединены между собой жестко, т. е. представляют собой одно звено и вращаются с одной угловой скоростью.

Далее переходим к построению линии распределения скоростей сателлита 5, который сопряжен с центральными колесами 4 и 6.

В полюсе зацепления 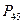колеса 5 с колесом 4 скорости обоих колес одинаковы, но скорость колеса 4 равна нулю, так как это колесо неподвижно. Поэтому и скорость колеса 5 в полюсе зацепления также равна нулю. На вертикальной оси отмечаем точку 4,5. Так как скорости сателлита 5 и водила «а» в точке, лежащей на оси сателлита одинаковы, то отрезок скорости водила «а» является и скоростью сателлита 5, введем дополнительное обозначение . Для получения линии распределения скоростей сателлита соединяем прямой точку 4,5 и конец отрезка скорости , .

В полюсе зацепления колеса 6 с колесом 5 скорости обоих колес одинаковы. Скорость колеса 6 определяется отрезком 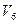, проведенным горизонтально на уровне полюса зацепления от вертикальной оси 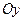до пересечения с линией распределения скоростей сателлита 5. Так как скорость колеса 6 на центральной оси равна нулю, то линию распределения скоростей получаем, соединяя конец отрезка 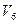с началом координат. Эта линия будет и линией распределения скоростей водила «в», т.к. водило «в» и колесо 6 соединены между собой жестко, т. е. представляют собой одно звено и вращаются с одной угловой скоростью.

Далее переходим к построению линии распределения скоростей колеса 2, которое сопряжено с колесами 1 и 3.

На этом сателлите можно найти скорости двух его точек и, следовательно, построить его линию распределения скоростей.

Скорость сателлита 2 в полюсе его зацепления с колесом 3 равна скорости колеса 3, а на оси равна скорости водила «в». Скорость колеса 2 в плюсе определяется отрезком , проведенным горизонтально на уровне полюса зацепления от вертикальной оси 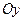до пересечения с линией распределения скоростей 3 колеса. Этот же отрезок изображает и скорость колеса 3 в полюсе зацепления с сателлитом 2.

Так как скорости сателлита 2 и водила «в» в точке, лежащей на оси сателлита одинаковы, то отрезок скорости водила «в» является и скоростью сателлита 2. Скорость водила «в» определяется отрезком , проведенным горизонтально на уровне оси сателлита 2 от вертикальной оси 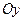до пересечения с линией распределения скоростей водила «в», введем дополнительное обозначение .

Для получения линии распределения скорости сателлита 2 соединяем концы отрезков ,и , .

В полюсе зацепления колеса 1 с колесом 2 скорости обоих колес одинаковы. Скорость колеса 1 определяется отрезком , проведенным горизонтально на уровне полюса зацепления от вертикальной оси 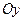до пересечения с линией распределения скоростей сателлита 2. Так как скорость колеса 1 на центральной оси равна нулю, то линию распределения скоростей получаем, соединяя конец отрезка с началом координат.

В произвольном месте картины скоростей проводим горизонталь , обозначаем точки её пересечения с линиями распределения скоростей центрального колеса 1 и водила «в», а также с вертикальной осью и находим передаточное отношение:

.

Дата добавления: 2014-01-07