Конические зубчатые передачи. 1. Общие сведения и характеристика

Лекция 4

1. Общие сведения и характеристика

2. Геометрические параметры

3. Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому

4. Силы зацепления прямозубой конической передачи

1. «Общие сведения и характеристика»

Конические зубчатые передачи передают механическую энергию между валами с пересекающимися осями.

Конические колеса обычно выполняют прямозубыми или с круговыми зубьями. Прямозубые передачи в основном применяют при окружных скоростях до 3 м/с, при более высоких скоростях применяют передачи с круговыми зубьями. Конические колеса с косыми зубьями применяют весьма редко из-за сложности изготовления и контроля.

Рис. 1

Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колес требуются специальные станки и специальный инструмент. Кроме допусков на размеры зубьев здесь необходимо выдерживать допуски на углы Σ [сигма], δ₁ и δ₂ [дельта], а при монтаже обеспечивать совпадение вершин конусов. Выполнить коническое зацепление с той же степенью точности, что и цилиндрическое, значительно труднее. Пересечение осей валов затрудняет размещение опор. Одно из конических колес располагают консольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба. В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, конические передачи имеют широкое применение, поскольку по условиям компоновки механизмов иногда необходимо располагать валы под углом.

2. «Геометрические параметры»

Рис. 2

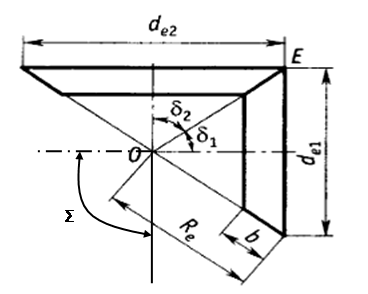
Углы делительных конусов связаны с их диаметрами (и числами зубьев z). Согласно рис. 1.

,

δ₂ = 90º - δ₁. [дельта]

Модуль конического колеса меняется по длине зуба. За основной принимают окружной модуль на внешнем торце m_te, который удобно измерять.

Внешние делительные диаметры (рис. 1)

d_e1 = m_tez₁, d_e2 = m_tez₂

Внешнее конусное расстояние R_e

Конусное расстояние до середины зуба (рис. 2)

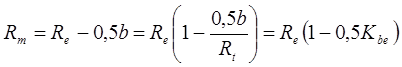
где - коэффициент ширины зубчатого венца. Значение К_bе ≤ 0,35 (обычно 0,285).

Средний делительный диаметр и модуль находят из соотношения для подобных треугольников:

d_m = d_e (1 – 0,5K_be)

m_m = m_te (1 – 0,5K_be)

Диаметры вершин зубьев (рис. 2)

d_ae = d_e + 2h_aecos δ [дельта]

Диаметр эквивалентного зубчатого колеса (рис. 2)

d_v = 2O₁E = d_e/cos δ

Эквивалентное число зубьев из зависимости [δ - дельта]

Передаточное отношение 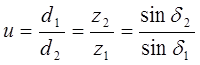при 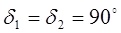- эта формула необходима для определения углов δ₁ и δ₂ [дельта].

Дата добавления: 2014-01-07