Конструирование планетарной передачи

Для компенсации погрешностей изготовления деталей передачи одно из центральных колес дел ают самоустанавливающимся (плавающим).На схеме плавающее звено – центральная шестерня. В радиальном направлении эта шестерня само устанавливается по сателлитам. В осевом направлении шестерню фиксируют с одной стороны торцы штыря 1, а с другой – зубчатой муфты 2 с установленными в ней пружинными кольцами 3. Делительный диаметр зубчатой муфты 2 принимают, для простоты изготовления, равным диаметру центральной шестерни. Диаметр муфты; ширина зацепления; толщина неподвижного колеса. где - модуль зацепления (мм), - ширина зубчатого венца.

Входной вал установлен на шариковых радиальных однорядных подшипниках с канавками на наружных кольцах. и вставленными в них установочными кольцами, применение которых упрощает осевое крепление подшипников в корпусе (крышке) и позволяет выполнять сквозную обработку отверстия корпуса (крышки).

Подшипники установлены по схеме в растяжку. Подшипники установлены один от другого на расстоянии. Концы валов выполняют – любой вариант.

Ведущий входной вал получает движение от электродвигателя (через соединительную муфту), полумуфту которой устанавливают на конической или цилиндрической выступающей конец вала.

При конструировании мотор – редуктора зубчатую муфту 1 соединяют непосредственно с шестерней 2, установленной на валу фланцевого электродвигателя.

Что бы сателлиты само устанавливались по неподвижному центральному колесу, необходимо применять сферические шариковые подшипники. При больших радиальных нагрузках вместо шариковых применяют роликовые сферические подшипники. Толщина обода сателлита.

Выходной вал редуктора выполняют литым из высокопрочного чугуна марки ВЧ50 и ВЧ60 за одно с водилом. или при мелкосерийном производстве – из стали и соединяют его с водилом сваркой, посадкой с натягом, шпоночным или шлицевым соединением.

Водило выполняют целыми литыми из стали и высокопрочного чугуна, сварным, составным (скрепленным шестью винтами и тремя штифтами).Диски сварного водила обычно выполняют круглыми (возможно равносторонни треугольником).

Задача: Рассчитать планетарную передачу

Привод с планетарным редуктором при нормальная мощность на исполнительном валу Р_Т = 1,5 кВт; частота вращения этого вала

n_T = 16 мин^-1; синхронная частота вращения электродвигателя n_c = 750 мин^-1

1. Кинематический и силовой расчет привода.

1.1.Определяем общий КПД привода по формуле, приняв по рекомендациям табл. КПД планетарного редуктора с раздвоенным сателлитом η_P = 0,95

1.2.Определяем потребную мощность электродвигателя

P_дв = P_T/η_P = 1,0 /0,95 = 1,05кВт:

1.3. По рекомендации принимаем двигатель с параметрами Р_дв = 1,1кВт,

n = 715мин^-1

1.4. Определяем общее передаточное число привода

u = n_дв/n_p = 715/16 = 44,68; u₁₂ = 12,5; u₂₃ = 44,68/12,5 = 3,57

1.5. Из единого ряда передаточных чисел для планетарного редуктора с двухвенцовым сателлитом u_p = 12, 5.

1.6. Определяем частоты вращения и угловые скоростu

- ведущий вал редуктора n₁ = n_дв

ω₁ = π n₁/30 = 3,14·715/30 = 74,83с^-1

ведомого вала – водило редуктора

– n₂ = n_h = n_T = n₁/u_p= 715/12,5 = 57,2мин

ω₂ = ω_h = ω₁/u_p = 74,83/12,5 = 5,98с^-1

1.7. Определяем вращающие моменты на валах привода

– на ведомом валу – водиле редуктора

T₂ = T_h = P_T/ω₂ = 1,5 /5,98 = 0,25Н.м.

- на ведущем валу редуктора

T₁ = T₂/u_p η_p = 0,25/(12,5·0,95)= 0,02Н.м.

Для принятого передаточного отношения по таблице выбираем вариант передачи с тремя двухвенцовыми сателлитами В₁³

Из условия подрезания принимаем число зубьев центрального солнечного колеса Z₁ = 18 По таблице определяем интерполированием значение коэффициента c = 1,52 и затем число зубьев центрального колеса с внутренними зубьями: Z₃ = Z₁(u₁³_h -1)/c = 18(12,5 - 1) = 207

Учитывая, что оно должно быть кратным числу сателлитов, принимаем

- Z₃ = 207. Уточняем значение коэффициента с:

c = Z₁ (u₁³_h – 1)/Z₃ = 18(12,5 - 1)/207 = 1,52

и определяем числа зубьев венцов сателлита:

Z₄ = (Z₃ – Z₁)/(c + 1)= (209-18)/(1,52 +1)= 75;

Z₂ = c Z₄= 1,52 75= 114

Принимая модули внешнего m₁₂ и внутреннего m ₂₄ зацеплений одинаковыми, из условия соосности уточняем число зубьев:

Z₂ = Z₃ – Z₄ – Z₁ = 207 – 75 – 18 = 114

Проверяем правильность подбора зубьев:

- из условия соосности уточняем число зубьев:

Z₁ + Z₂ = Z₃ – Z₄ = 18 + 114 = 207 – 75 = 132

- условие сборки Z₁/n_w = 18/3 = 6 Z₃ /n_w = 207/3=69

n_w – число сателлитов (3)

- условие соседства:

для внешнего зацепления (Z₁ + Z₂)sin(π/n_w) – Z₂ › 2

(18+114)Sin(180/3) -114 = 2,6

для внутреннего зацепления (Z₃ – Z₄)sin(π/n_w) – Z₄

(207 - 75)Sin(180/3) – 75= 4,01

Если условия выполняются - числа зубьев определены правильно.

Уточняем передаточное отношение:

Знак - показывает, что направления вращения водила и сателлита вокруг своих осей противоположны.

2. Определяем коэффициент полезного действия передачи, предварительно определив передаточное отношение u₁^h₃ при ω_h = 0 и приняв коэффициент потерь ψ^h = 0,03

u₁^h₃ = -Z₂Z₃/(Z₁Z₄)= 114·207/18·75 = 17,48

η₁³_h = η_h³₁ = 1 – u₁^h₃ψ^h/(u₁^h₃ -1)=17,48

Определяем расчетный момент на колесе, предварительно находя моменты, действующие на основные звенья планетарной передачи, принебрегая потерями на трение:

T₁ = -T_hZ₁Z₄/(Z₁Z₄ +Z₂Z₃) = - (62,84·18·75)/(18·75+208·114) =

-3,41H.M.

Момент на колесе с числом зубьев внутреннего зацепления

T₃ = -T_hZ₂Z₃/(Z₁Z₄+Z₂Z₃) = -62,84·208·114/(18·75+207·114)=

-59,726Н.м.

Проверяем правильность вычисления моментов:

T_h + T₃ + T₁ = 0

T_h = -T₁u₁³_h = 1,48·18,48 = 27,35Н.м.

T_h = -T₃u₃¹_h = 0,12·13,05 = 1,57Н.м.

где U₃¹_h = (ω₃ – ω₁)/(ω_h - 1) = 298,3/(23,86-1)=13,05

ω₃ = 0; момент на ведущем валу редуктора с учетом потерь на трение, приняв коэффициентΨ_n = 0,98

T₁ = -T_h/(u₁³_h η₁³_h ψ_n) = -1,48/(17,48·13,05·0,98)= 0,28

Расчетный на колесе (на зубчатом венце с числом зубьев Z₂ наиболее нагруженного сателлита):

T₂ = T₁u₁^h₂Ω/n_w = 0,12·(114/18)1,2/3 = 0,7

где u₁^h₂ = Z₂/Z₁, что соответствует стандартному значению

Ω = 1,2 – коэффициент, учитывающий неравномерность распределения нагрузки

3. Выбираем материал колес и определяем допускаемые напряжения. По таблице сталь (50ХН nо таблице принимаем пределы контактной и изгибной выносливости:

σ_Hlim1 = σ_Hlim2 = σ_Hlim = 17HRC + 200 = 17 53 + 200 = 1100МПа

σ_Flim = 650МПа

Относительная угловая скорость солнечного центрального колеса (шестерни с числом зубьев Z₁)

ω₁^h = ω₁ – ω_h = 298,3-23,86 = 274,84

Относительная угловая скорость сателлита

ω₂^h = ω₂ –ω_h =23,86 -23,86 = 0

Суммарное число циклов нагружения для солнечного колеса:

N_k = 573ω₁^h L_h n_w > N_{Hli m} = 100·10⁶

Для сателлитов:

N_k = 573ω₂^h L_h < N_Hlim = 100·10⁶ - число циклов нагружения, соответствующее пределу выносливости, определенное интерполированием;

L_h = 20·10³ – ресурс передачи;

Определяем коэффициент долговечности:

Z_N = 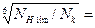S_Hlim = 1,2

Находим допускаемые контактные напряжения принимая для зубчатых колес с поверхностным упрочнением

σ_HP = (σ_Hlim/S_H)Z_N = (1100/1,2)1,1 =1008

Вычисляем допускаемое напряжение изгиба при расчете на контактную прочность зубьев, принимая S_Flim =1,75 для зубчатых колес, изготовленных из поковок и штамповок, Y_α = 0,8, при двухстороннем приложении нагрузки и Y_N = 1 при N_Flim = N_{H lim} > 4·10⁶

σ_Fp = (σ_Flim/S_Flim)Y_α Y_N = (650/1,75)0,8·1,0 = 297,14

Определяем коэффициент ширины венца

Ψ_ba = [1,5 + 0,1(3-n_w)]/(u₁^h₂ +1) = 1,5

Полученное значение округляем до стандартного ψ_{ba =}1,5

Принимая предварительно коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса, К_Нβ = 1,42, интерполированием по таблице для выбранной схемы при

b/d₁ = ψ_ba(u₁^h₂ - 1)/2 и коэффициент К_а = 49,5 – для прямозубой передачи определяем расстояния а_w12 и а _w34 между осями центральных колес и сателлитов

a_w12 ≥ K_a(u₁^h₂ + 1 ) 98,8 = 100мм

a_w34 ≥ K_a(u₄^h₃ + 1) 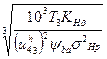= 148,6 = 150мм

где u₄^h₃ = Z₃/Z₄= 209/75 = 2,78

Для обеспечения равно прочности внешнего и внутреннего зацеплений и экономии дорогой стали 50ХН для колеса с внутренними зубьями назначаем конструкционную легированную сталь 40Х, термообработка – улучшение с последующей закалкой ТВЧ. Тогда расчетное контактное напряжение

σ_Hp = (σ_Hlim/S_Hlim)Z_N a_w34 = 150мм

Определяем модуль зацепления

m = 2a_w12/(Z₁ + Z₂)= 1,5мм

Принимаем m = 1,5мм

Уточняем межосевое расстояние

a_w12 = m(Z₁ + Z₂)/2 = 100мм

Определяем ширину зубчатых венцов сателлита:

b₂ = b₄ = ψ_baa_w12 = 1,5 100 = 150мм

Округляем значение до стандартного. Принимаем b₂ = b₄ =150мм

Ширину венца центральных колес принимаем на 3…5 мм больше ширины венца сателлита: b₁ = b₃ = b₂ + 3…5

Вычисляем диаметры колес с внешним зацепление

- делительные диаметры d₁ = mZ₁ = 1,5 18 = 27мм

d₂ = mZ₂ = 1,5 114 = 171мм

d₄ = mZ₄ = 1,5 75 = 112,5мм

-диаметры окружностей вершин зубьев

d_a1 = d₁ + 2m = 27 + 3 = 30мм

d_a2 = d₂ + 2m = 171 + 3 = 174мм

d_a4 = d₄ + 2m = 112,5 + 3 = 115,5мм

- диаметры окружностей впадин зубьев

d_f1 = d₁ – 2,5m = 27 – 3,75 = 23,25мм

d_f2 = d₂ – 2,5m = 171 – 3,75 = 167,25мм

d_f4 = d₄ – 2,5m = 112,5 – 3,75 = 108,75мм

Определяем диаметры колес с внутренними зубьями

d₃ = mZ₃ = 1,5 209 = 313,5мм

d_a3 = d₃ -2m +15,2m/Z₃=313,5- 3,0 + 0,12 = 310,62мм

d_f3 = d₃ +2,5m =313,5 + 3,75 = 317,25мм

Уточняем межосевое расстояние

a_w12 = (d₁ + d₂)/2 = (27 + 171)/2 = 99

a_w34 = (d₃ – d₄)/2 =100,25мм

4. Определяем нормальные силы в зацеплении

F_n1 = 2T₁/(d₁cosα) = F_n2 = 2 1,48/(27 cos20⁰) = 0,6Н

F _n3 = 2T₃/(d₃cosα) = F_n4 = 27,35/(313,5cos20⁰) = 0.4Н

Определяем нагрузки,действующие на ось наиболее нагруженного сателлита:

- окружная сила во внешнем зацеплении:

F _t1 = (2T₁/n_wd₁)Ω= (2·1,48/3·27)1,2 = 0,44Н

- радиальная сила:

F _r1 = F^t₁tgα = 156tg20⁰ = 1,2Н

- окружная сила во внутреннем зацеплении

F t₃ =(2T₃/n_wd₃)Ω = (2·27,35/313,5)1,2 = 23Н

Радиальная сила

F r₃ = F^t₃tgα = 23tg20⁰= 17Н

Задача: Рассчитать планетарную передачу

Привод с планетарным редуктором при нормальная мощность на исполнительном валу Р_Т = 1,22 кВт; частота вращения этого вала

n_T = 14 мин^-1; синхронная частота вращения электродвигателя n_c = 1000 мин^-1

2. Кинематический и силовой расчет привода.

1.1.Определяем общий КПД привода по формуле, приняв по рекомендациям табл. КПД планетарного редуктора с раздвоенным сателлитом η_P = 0,95

1.2.Определяем потребную мощность электродвигателя

P_дв = P_T/η_P = 1,22 /0,95 = 1,35кВт:

1.3. По рекомендации принимаем двигатель с параметрами Р_дв = 1,5кВт,

n = 925мин^-1

1.4. Определяем общее передаточное число привода

u = n_дв/n_p = 925/14 = 66; u₁₂ = 12,5; u₂₃ = 66/12,5 = 5,28.

1.5. Из единого ряда передаточных чисел для планетарного редуктора с двухвенцовым сателлитом u_p = 12, 5.

1.6. Определяем частоты вращения и угловые скоростu

- ведущий вал редуктора n₁ = n_дв

ω₁ = π n₁/30 = 3,14·925/30 = 96,8с^-1

ведомого вала – водило редуктора

– n₂ = n_h = n_T = n₁/u_p= 925/12,5 = 74,0мин

ω₂ = ω_h = ω₁/u_p = 96,8/12,5 = 7,7с^-1

2.Определяем вращающие моменты на валах привода

– на ведомом валу – водиле редуктора

T₂ = T_h = P_T/ω₂ = 1,22 /7,7 = 0,158Н.м.

- на ведущем валу редуктора

T₁ = T₂/u_p η_p = 0,158/(12,5 0,95)= 0,1Н.м.

Для принятого передаточного отношения по таблице выбираем вариант передачи с тремя двухвенцовыми сателлитами В₁³

Из условия подрезания принимаем число зубьев центрального солнечного колеса Z₁ = 18 По таблице определяем интерполированием значение коэффициента c = 1,52 и затем число зубьев центрального колеса с внутренними зубьями: Z₃ = Z₁(u₁³_h -1)/c = 18(12,5 - 1) = 207

Учитывая, что оно должно быть кратным числу сателлитов, принимаем

- Z₃ = 207. Уточняем значение коэффициента с:

c = Z₁ (u₁³_h – 1)/Z₃ = 18(12,5 - 1)/207 = 1,52

и определяем числа зубьев венцов сателлита:

Z₄ = (Z₃ – Z₁)/(c + 1)= (209-18)/(1,52 +1)= 75;

Z₂ = c Z₄= 1,52 75= 114

Принимая модули внешнего m₁₂ и внутреннего m ₂₄ зацеплений одинаковыми, из условия соосности уточняем число зубьев:

Z₂ = Z₃ – Z₄ – Z₁ = 207 – 75 – 18 = 114

Проверяем правильность подбора зубьев:

- из условия соосности уточняем число зубьев:

Z₁ + Z₂ = Z₃ – Z₄ = 18 + 114 = 207 – 75 = 132

- условие сборки Z₁/n_w = 18/3 = 6 Z₃ /n_w = 207/3=69

n_w – число сателлитов (3)

- условие соседства:

для внешнего зацепления (Z₁ + Z₂)sin(π/n_w) – Z₂ › 2

(18+114)Sin(180/3) -114 = 2,6

для внутреннего зацепления (Z₃ – Z₄)sin(π/n_w) – Z₄

(207 - 75)Sin(180/3) – 75= 4,01

Если условия выполняются - числа зубьев определены правильно.

Уточняем передаточное отношение:

u₁³_h = =1+ (207·114/18·75) =18,48

Определяем угловую скорость сателлтита

ω₂ = ω₄ = ω_h – (Z₃/Z₄)ω_h = -7,7 – (207/75)7,7= -13,55

Знак - показывает, что направления вращения водила и сателлита вокруг своих осей противоположны.

2. Определяем коэффициент полезного действия передачи, предварительно определив передаточное отношение u₁^h₃ при ω_h = 0 и приняв коэффициент потерь ψ^h = 0,03

u₁^h₃ = -Z₂Z₃/(Z₁Z₄)= 114·207/18·75 = 17,48

η₁³_h = η_h³₁ = 1 – u₁^h₃ψ^h/(u₁^h₃ -1)=17,48

Определяем расчетный момент на колесе, предварительно находя моменты, действующие на основные звенья планетарной передачи, принебрегая потерями на трение:

T₁ = -T_hZ₁Z₄/(Z₁Z₄ +Z₂Z₃) = - (0,158·18·75)/(18·75+208·114) =

-0,341H.M.

Момент на колесе с числом зубьев внутреннего зацепления

T₃ = -T_hZ₂Z₃/(Z₁Z₄+Z₂Z₃) = -0,158·208·114/(18·75+207·114)=

-5,9726Н.м.

Проверяем правильность вычисления моментов:

T_h + T₃ + T₁ = 0

T_h = -T₁u₁³_h = 0,341·18,48 = 27,35Н.м.

T_h = -T₃u₃¹_h = 5,97·13,05 = 1,57Н.м.

где U₃¹_h = (ω₃ – ω₁)/(ω_h - 1) = 298,3/(7.7-1)=13,05

ω₃ = 0; момент на ведущем валу редуктора с учетом потерь на трение, приняв коэффициентΨ_n = 0,98

T₁ = -T_h/(u₁³_h η₁³_h ψ_n) = -0,158/(17,48·13,05·0,98)= 0,28

Расчетный на колесе (на зубчатом венце с числом зубьев Z₂ наиболее нагруженного сателлита):

T₂ = T₁u₁^h₂Ω/n_w = 0,12·(114/18)1,2/3 = 0,7

где u₁^h₂ = Z₂/Z₁, что соответствует стандартному значению

Ω = 1,2 – коэффициент, учитывающий неравномерность распределения нагрузки

3. Выбираем материал колес и определяем допускаемые напряжения. По таблице сталь (50ХН nо таблице принимаем пределы контактной и изгибной выносливости:

σ_Hlim1 = σ_Hlim2 = σ_Hlim = 17HRC + 200 = 17 53 + 200 = 1100МПа

σ_Flim = 650МПа

Относительная угловая скорость солнечного центрального колеса (шестерни с числом зубьев Z₁)

ω₁^h = ω₁ – ω_h = 298,3-7,7 = 290,7

Относительная угловая скорость сателлита

ω₂^h = ω₂ –ω_h =7,7 -7,7 = 0

Суммарное число циклов нагружения для солнечного колеса:

N_k = 573ω₁^h L_h n_w > N_{Hli m} = 100·10⁶

Для сателлитов:

N_k = 573ω₂^h L_h < N_Hlim = 100·10⁶ - число циклов нагружения, соответствующее пределу выносливости, определенное интерполированием;

L_h = 20·10³ – ресурс передачи;

Определяем коэффициент долговечности:

Z_N = 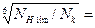S_Hlim = 1,2

Находим допускаемые контактные напряжения принимая для зубчатых колес с поверхностным упрочнением

σ_HP = (σ_Hlim/S_H)Z_N = (1100/1,2)1,1 =1008

Вычисляем допускаемое напряжение изгиба при расчете на контактную прочность зубьев, принимая S_Flim =1,75 для зубчатых колес, изготовленных из поковок и штамповок, Y_α = 0,8, при двухстороннем приложении нагрузки и Y_N = 1 при N_Flim = N_{H lim} > 4·10⁶

σ_Fp = (σ_Flim/S_Flim)Y_α Y_N = (650/1,75)0,8·1,0 = 297,14

Определяем коэффициент ширины венца

Ψ_ba = [1,5 + 0,1(3-n_w)]/(u₁^h₂ +1) = 1,5

Полученное значение округляем до стандартного ψ_{ba =}1,5

Принимая предварительно коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса, К_Нβ = 1,42, интерполированием по таблице для выбранной схемы при

b/d₁ = ψ_ba(u₁^h₂ - 1)/2 и коэффициент К_а = 49,5 – для прямозубой передачи определяем расстояния а_w12 и а _w34 между осями центральных колес и сателлитов

a_w12 ≥ K_a(u₁^h₂ + 1 ) 98,8 = 100мм

a_w34 ≥ K_a(u₄^h₃ + 1) 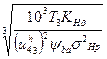= 148,6 = 150мм

где u₄^h₃ = Z₃/Z₄= 209/75 = 2,78

Для обеспечения равно прочности внешнего и внутреннего зацеплений и экономии дорогой стали 50ХН для колеса с внутренними зубьями назначаем конструкционную легированную сталь 40Х, термообработка – улучшение с последующей закалкой ТВЧ. Тогда расчетное контактное напряжение

σ_Hp = (σ_Hlim/S_Hlim)Z_N a_w34 = 150мм

Определяем модуль зацепления

m = 2a_w12/(Z₁ + Z₂)= 1,5мм

Принимаем m = 1,5мм

Уточняем межосевое расстояние

a_w12 = m(Z₁ + Z₂)/2 = 100мм

Определяем ширину зубчатых венцов сателлита:

b₂ = b₄ = ψ_baa_w12 = 1,5 100 = 150мм

Округляем значение до стандартного. Принимаем b₂ = b₄ =150мм

Ширину венца центральных колес принимаем на 3…5 мм больше ширины венца сателлита: b₁ = b₃ = b₂ + 3…5

Вычисляем диаметры колес с внешним зацепление

- делительные диаметры d₁ = mZ₁ = 1,5 18 = 27мм

d₂ = mZ₂ = 1,5 114 = 171мм

d₄ = mZ₄ = 1,5 75 = 112,5мм

-диаметры окружностей вершин зубьев

d_a1 = d₁ + 2m = 27 + 3 = 30мм

d_a2 = d₂ + 2m = 171 + 3 = 174мм

d_a4 = d₄ + 2m = 112,5 + 3 = 115,5мм

- диаметры окружностей впадин зубьев

d_f1 = d₁ – 2,5m = 27 – 3,75 = 23,25мм

d_f2 = d₂ – 2,5m = 171 – 3,75 = 167,25мм

d_f4 = d₄ – 2,5m = 112,5 – 3,75 = 108,75мм

Определяем диаметры колес с внутренними зубьями

d₃ = mZ₃ = 1,5 209 = 313,5мм

d_a3 = d₃ -2m +15,2m/Z₃=313,5- 3,0 + 0,12 = 310,62мм

d_f3 = d₃ +2,5m =313,5 + 3,75 = 317,25мм

Уточняем межосевое расстояние

a_w12 = (d₁ + d₂)/2 = (27 + 171)/2 = 99

a_w34 = (d₃ – d₄)/2 =100,25мм

4. Определяем нормальные силы в зацеплении

F_n1 = 2T₁/(d₁cosα) = F_n2 = 2 1,48/(27 cos20⁰) = 0,6Н

F _n3 = 2T₃/(d₃cosα) = F_n4 = 27,35/(313,5cos20⁰) = 0.4Н

Определяем нагрузки,действующие на ось наиболее нагруженного сателлита:

- окружная сила во внешнем зацеплении:

F _t1 = (2T₁/n_wd₁)Ω= (2·1,48/3·27)1,2 = 0,44Н

- радиальная сила:

F _r1 = F^t₁tgα = 156tg20⁰ = 1,2Н

- окружная сила во внутреннем зацеплении

F t₃ =(2T₃/n_wd₃)Ω = (2·27,35/313,5)1,2 = 23Н

Радиальная сила

F r₃ = F^t₃tgα = 23tg20⁰= 17Н

Дата добавления: 2014-01-07