Лекция 2. NP-полные задачи

Если 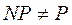, тогда в класс NP входят кроме класса Р и другие задачи.

Различают еще NPC - NP- полные задачи и NPI – задачи.

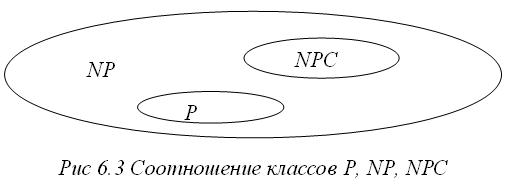
Таким образом:

Здесь

Р – простые задачи,

NPC – сложные задачи,

NPI – промежуточный класс задач.

Рассмотрим класс NPC – NP-полные задачи или проблемы.

Опр. Проблема Т называется NP-полной, если она удовлетворяет 2-м условиям:

1.

2. Если 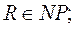то R сводится к Т за полиномиальное время, т.е. к ней полиномиально должны сводиться все задачи из класса NP.

Понятие NP-полноты было введено независимо Куком (Stephen Cook, 1971) и Левиным (1973) и основывается на понятии сводимости одной за дачи к другой.

В теории сложности вычислений принято говорить, что задача задается некоторым языком, тогда если задача 1 задана языком L1, а задача 2 - языком

L2, то полиномиальная сводимость языков, задающих задачи, обозначается следующим образом: .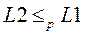

NP-полные проблемы являются универсальными. Не нужно придумывать алгоритмы для всех задач, достаточно свести эту задачу к какой-либо NP-полной задаче.

Если же любую из NP-полных задач удастся свести к задаче класса Р, то и все NP задачи получат полиномиальное решение.

Для класса NPC доказана следующая теорема:

Теорема. Если существует задача, принадлежащая классу NPC, для которой существует полиномиальный алгоритм решения, то класс Р совпадает с классом NP, т.е. P = NP

Схема доказательства состоит в сведении с полиномиальной трудоемкостью любой задачи из класса NP к данной задаче из класса NPC и решении этой задачи за полиномиальное время (по условию теоремы).

В настоящее время доказано существование сотен NP-полных задач, но ни для одной из них пока не удалось найти полиномиального алгоритма решения. Отметим, что для многих из них предложены приближенные полиномиальные алгоритмы.

Сегодня ученые предполагают следующее соотношение классов 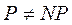то есть , и ни одна задача из класса NPC не может быть решена, по крайней мере, сегодня, с полиномиальной сложностью.

Термин NP-полная относится к самым сложным задачам в классе NP. Мы показываем, что задача является NP-полной, указывая способ сведения к ней всех остальных задач класса NP. На практике эта деятельность выглядит не столь уж устрашающе - нет необходимости осуществлять редукцию для каждой NP задачи. Вместо этого для того, чтобы доказать NP-полноту некоторой NP задачи А, достаточно свести к ней какую-нибудь NP-полную задачу В. Редуцировав задачу В к задаче А, мы показываем, что и любая NP задача может быть сведена к А за два шага, первый из которых — ее редукция к В.

Рассмотрим редукцию алгоритма, решающего NP задачу. Нам понадобится процедура, которая преобразует все составные части задачи в эквивалентные составные части другой задачи. Такое преобразование должно сохранять информацию: всякий раз, когда решение первой задачи дает положительный ответ, такой же ответ должен быть и во второй задаче, и наоборот.

Гамильтоновым путем в графе называется путь, проходящий через каждую вершину в точности один раз. Если при этом путь возвращается в исходную вершину, то он называется гамильтоновым циклом.

Граф, в котором есть гамильтонов путь или цикл, не обязательно является полным. Задача о поиске гамильтонова цикла следующим образом сводится к задаче о коммивояжере. Каждая вершина графа — это город. Стоимость пути вдоль каждого ребра графа положим равной 1.Стоимость пути между двумя городами, не соединенными ребром, положим равной 2. А теперь решим соответствующую задачу о коммивояжере. Если в графе есть гамильтонов цикл, то алгоритм решения задачи о коммивояжере найдет циклический путь, состоящий из ребер веса 1. Если же гамильтонова цикла нет, то в найденном пути будет по крайней мере одно ребро веса 2. Если в графе N вершин, то в нем есть гамильтонов цикл, если длина найденного пути равна N, и такого цикла нет, если длина найденного пути больше N.

Дата добавления: 2014-01-07