Математические модели вентильных преобразователей

ЛЕКЦИЯ 11

Вид математической модели вентильного преобразователя су­щественно определяет выбор метода расчета электромагнитных процессов в нем. Метод расчета, в свою очередь, определяет тру­доемкость вычислений и вид полученного результата. Поэтому выбор математических моделей вентиля и преобразователя, а так­же метода расчета процессов в преобразователе необходимо де­лать согласованно.

Периодическая коммутация вентилей в преобразователе (мо­дель вентиля в виде ключа) приводит к двум видам математичес­ких моделей преобразователя. Если на входе преобразователя ис­пользуются модели идеальных источников ЭДС и тока, а внутри вентильного комплекта нет пассивных элементов электрической цепи (сопротивлений, конденсаторов, реакторов), то вентильный преобразователь совместно с входным источником замещается ис­точником напряжения или тока разрывной формы в соответствии с первыми уравнениями систем (1.4.2) и (1.4.3). Тогда процессы в нагрузке описываются дифференциальными уравнениями с посто­янными коэффициентами и разрывной правой частью. Если на входе или внутри вентильного преобразователя имеются пассив­ные элементы (например, элементы фильтров), то процессы в на­грузке и во входных цепях преобразователя описываются диффе­ренциальными уравнениями с переменными периодическими (раз­рывными) коэффициентами. В таком случае анализ процессов в преобразователе существенно усложняется (см. гл. 5).

Для обеих математических моделей вентильных преобразова­телей применимы следующие три метода расчета энергетических показателей преобразователей: 1) интегральный; 2) спектральный; 3) прямой.

МЕТОДЫ РАСЧЕТА ЭНЕРГЕТИЧЕСКИХ ПОКАЗАТЕЛЕЙ

ИНТЕГРАЛЬНЫЙ МЕТОД

В интегральном методе расчета относительных энергетических показателей все абсолютные величины, которые входят в эти пока­затели, выражаются в форме определенных интегралов от соответ­ствующих токов, напряжений и их комбинаций. Это действующие значения токов и напряжений

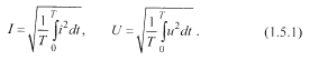
Это активная мощность

реактивные мощности сдвига (при синусоидальной форме напря­жения или тока)

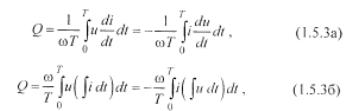
полная мощность

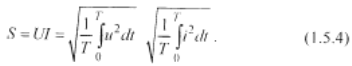
Для углубленной характеристики несинусоидальных энерго­процессов можно привлечь еще массу других парциальных со­ставляющих полной мощности, общее выражение для которых в интегральной форме имеет вид [20, 21, 39].

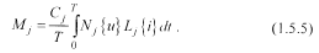
Здесь вид операторов преобразования напряжения Nj {и} и тока Lj {i} определяет и ту или иную парциальную составляющую Mj полной мощности S {см. гл. 6).

Для вычисления всех указанных интегралов необходимо знать законы изменения мгновенных значений соответствующих переменных. Они могут быть найдены только из решения диффе­ренциальных уравнений, составленных для электрической цепи, в которой вычисляются энергетические показатели. Это обстоя­тельство определяет следующие потребительские свойства интегрального метода расчета.

1. Метод универсален, так как дифференциальные уравнения всегда можно решить аналитически или численно.

2. При отсутствии аналитического решения дифференциально­го уравнения сам метод расчета энергетических показателей ста­новится численным. Это не позволяет провести общее исследова­ние в аналитической форме зависимости энергетических показате­лей от параметров электрической цепи.

3. При высоком порядке дифференциальных уравнений (выше 2-3) и наличии на периоде множества точек нарушения непрерывности функций, вызванных скачкообразным переключением вен­тилей, метод становится очень трудоемким и доступным только для ЭВМ.

СПЕКТРАЛЬНЫЙ МЕТОД

В спектральном методе расчета относительных энергетиче­ских показателей все абсолютные величины, которые входят в оп­ределение показателей, выражаются в форме бесконечных рядов, которые получаются из рядов Фурье (спектров) соответствующих токов и напряжений. Так, действующие значения напряжений и токов согласно формуле Парсеваля из теории рядов Фурье вычис­ляются следующим образом:

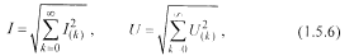
где I(k), U(к) - действующие значения гармоник k-го порядка тока и напряжения. Отсюда активная мощность

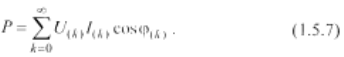
Реактивная мощность Боденю (сдвига) при несинусоидальных напряжениях и токах

Полная мощность

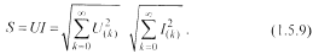
Для вычисления указанных величин необходимо знать спектры напряжения и тока в электрической цепи. Спектр напряжения на­ходится по известной форме кривой напряжения разложением ее в ряд Фурье. Спектр тока рассчитывается через спектр напряжения и найденные по схеме цепи полные сопротивления по каждой гармонике спектра. Эта процедура определяет потребительские свойства спектрального метода:

1. Метод не требует составления и решения дифференциаль­ных уравнений, что освобождает от соответствующих затрат вре­мени и

2.

3.

4. возможных ошибок.

5. Энергетические показатели представляются выражениями, содержащими бесконечные ряды. Практическое усечение ряда всегда вносит в расчет погрешность, которую оценить нелегко.

6. Параметры цепи входят в каждый член ряда, что затрудняет аналитическое исследование влияния отдельных параметров цепи на каждый энергетический показатель, делая процедуру расчета, по сути, численной.

ПРЯМЫЕ МЕТОДЫ

Прямые методы - методы алгебраизации дифференциальных уравнений. Под прямыми методами расчета энергетических пока­зателей в цепях с несинусоидальными напряжениями и токами по­нимают методы, не требующие ни нахождения мгновенных значе­ний тока (как в интегральном методе), ни нахождения его спектра (как в спектральном методе). Прямой метод, излагаемый здесь, назван методом алгебраизащш дифференциальных уравнений (АДУ) [21], расчетные формулы для энергетических показателей выводятся прямо через коэффициенты дифференциального урав­нения и параметры приложенного напряжения. В качестве таких параметров используется набор интегральных коэффициентов гармоник напряжения, полученный расширением определения традиционного коэффициента гармоник напряжения, как показано ниже.

Метод АДУ рассмотрим на примерах расчета цепей первого и второго порядка, к которым сводятся математические модели большинства изучаемых в курсе базовых ячеек преобразователей. При этом сам метод АДУ можно применять для расчета:

- действующего значения несинусоидального тока (метод АДУ1);

- действующего значения высших гармоник тока (метод АДУ2);

- первой гармоники тока (метод АДУ(1));

- мощностей, создаваемых всей кривой тока (метод АДУМ1), ее высокочастотной составляющей (метод АДУМ2), ее первой гармоникой (метод АДУМ(1)).

Дата добавления: 2014-01-07