Принцип образования плоских механизмов. Группы Ассура

Принцип образования механизмов, впервые сформулированный в 1916г. проф. Л. В. Ассуром, заключается в следующем. Любой механизм может быть получен путем присоединения к одному или нескольким начальным звеньям и стойке кинематических цепей (структурных групп) нулевой подвижности относительно тех звеньев, к которым группа присоединяется.

Кинематические цепи, обладающие нулевой степенью подвижности относительно внешних кинематических пар, называются группами Ассура.

Внешние кинематические пары – кинематические пары звеньев, которыми они впоследствии присоединяются к другим кинематическим цепям или звеньям.

В качестве первичного механизма (по И.А. Артоболевскому – механизм 1 класса) принимаем двухзвенный механизм, состоящий из ведущего звена 1 и стойки 0 (рис. 1).

Рис. 1. Первичный механизм (механизм 1 класса)

Для структурных групп Ассура, согласно определению и формулы Чебышева справедливо равенство:

(2.1)

Поскольку 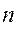и 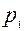могут быть только целыми числами, из равенства (2.1) получаются следующие сочетания:

а) , ;

б) , ;

в) 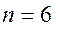, 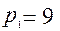и т. д.

Группы Ассура делятся на классы и порядки. Класс группы определяется числом кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами.

При этом двухповодковая структурная группа, не имеющая замкнутого контура, отнесена ко второму классу.

Порядок структурной группы определяется числом внешних кинематических пар.

Группа, имеющая два звена и три кинематические пары 5-го класса, называется группой 11 класса 2-го порядка или двухповодковой группой (см. рис.2,а). Второе возможное сочетание числа подвижных звеньев и кинематических пар образует группу 111 класса 3-го порядка, или трехповодковую (см. рис. 2,б). Пунктирной линией показаны звенья, к которым группа присоединяется. Этими звеньями являются начальное звено, или звенья других групп, или стойка.

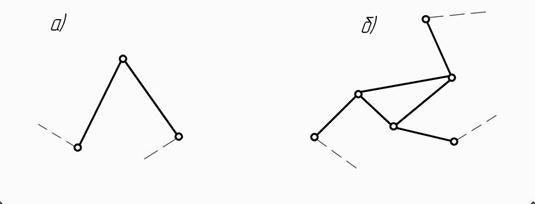ис 2. Примеры структурных групп: а – 11 класса; б – 111 класса

Рис 2. Примеры структурных групп: а – 11 класса; б – 111 класса

Класс механизма определяется наивысшим классом структурной группы, входящей в состав данного механизма.

Двухповодковая группа имеет 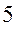видов в зависимости от сочетания вращательных и поступательных пар (рис.3):

1) группа вида – все пары вращательные;

2) группа вида – на конце одного из звеньев поступательная пара;

3) группа вида – в середине поступательная пара;

4) группа вида – на конце обоих звеньев поступательные пары;

5) группа 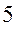вида – в середине и на конце одного из звеньев поступательная пара.

Рис. 3. Виды структурных групп 11 класса

Структурный анализ механизма следует проводить путем расчленения его на структурные группы в порядке, обратном образованию механизма.

Пример. Выполнить структурный анализ механизма четырезвенника (рис.4).

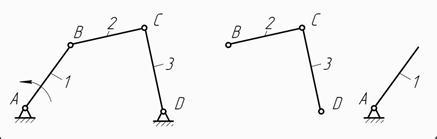
Рис.4. Структурная схема шарнирного четырехзвенника

1. Определяем степень подвижности механизма:

W= 3n – 2p₁ – p₂ = 3 · 3- 2 · 4 – 0 = 1.

2. Выделим группы Ассура (последние два звена и три кинематические пары) – группы 11 класса 1-го вида (11₁):

W= 3n – 2p₁ – p₂ = 3 · 2- 2 · 3 – 0 = 0.

3. Остается механизм 1 класса:

W = 3 × 1 – 2 × 1 = 1.

Данный механизм образован присоединением к первичному механизму 1 класса группы Ассура 11 класса 1-го вида, т.е. весь механизм является механизмом 11 класса.

Структура механизма записывается в следующей форме:

1 ® 11₁.

В зависимости от того, какое звено является ведущим, механизм может раскладываться на группы различного класса.

Пример механизма 111 класса показан на рис. 5.

Рис.5. Рычажный механизм 111 класса

Структурная формула механизма:

1® 111.

Дата добавления: 2014-01-07