Идеальный газ

Часть I. Молекулярно-кинетическая теория

Ч. I. молекулярно-кинетическая теория

МОЛЕКУЛЯРНАЯ Физика

Учебное пособие

Новосибирск

УДК 536.7

ББК В36я73-1

З 266

Дзюба С. А., Замураев В. П., Калинина А. П. Молекулярная физика. Ч. I. молекулярно-кинетическая теория/ Новосиб. гос. ун-т. Новосибирск, 2012. 106 с.

ISBN 978-5-94356-980-7

В учебном пособии изложены материалы по разделу «молекулярно-кинетическая теория» курса «Молекулярная физика», читаемого на первом курсе физического факультета НГУ. В пособии рассмотрены распределения Максвелла, Больцмана, Максвелла–Больцмана, Гиббса; на их основе изложены теория теплоемкости и основы явлений переноса в плотных и ультраразреженных газах.

Пособие предназначено для преподавателей и студентов вузов.

Издание подготовлено в рамках реализации Программы развития НИУ-НГУ на 2009–2018 годы.

Учебное пособие рекомендовано к изданию Ученым советом ИТПМ СО РАН.

Рецензент

д-р физ.-мат. наук, проф. С. С. Кацнельсон

© Новосибирский государственный университет, 2012

ã Дзюба С. А., Замураев В. П., Калинина А. П., 2012

Глава 1

Идеальный газ – это теоретическая модель газа, в которой пренебрегается взаимодействием между молекулами (за исключением взаимодействий в краткие моменты столкновений). В воздухе, например, среднее расстояние между молекулами примерно в 10³ раз больше их размера, поэтому действительно при рассмотрении многих явлений взаимодействием молекул можно пренебречь. Хорошим приближением к модели идеального газа является любой разреженный в достаточной степени реальный газ. Молекулы идеального газа в основном находятся в состоянии равномерного и прямолинейного движения. Все направления движения в отсутствие внешнего поля (или при его малости) равновероятны. Движение имеет хаотический характер, так как после каждого столкновения скорости и направления движения существенным образом меняются. Важно также подчеркнуть, что количество молекул в макроскопическом объеме газа огромное (порядка 3 10¹⁹ в см^–3 при обычных условиях).

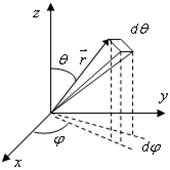
Рис. 1.1.

Выберем некоторое направление, характеризуемое углами θ и φ сферической системы координат (см. рис. 1.1). Пусть нас интересует доля молекул, движущихся именно в этом направлении. Вообще говоря, несмотря на огромное количество молекул, вероятность найти молекулу, движущуюся строго в данном направлении, равна нулю, так как направление задается бесконечно узкой линией, а число молекул все-таки конечно. Можно говорить только о вероятности иметь направление в интервалах углов от θ до θ + dθ и от φ до φ + dφ. Чем меньше dθ и dφ, тем точнее задается направление. Указанные две пары углов задают в пространстве четыре радиус-вектора, которые на единичной сфере (см. рис. 1.1) определяют вершины криволинейного четырехугольника малой площади dS = sin θ dθ dφ = dΩ, где dΩ – элемент так называемого телесного угла. Вероятность попадания единичного вектора, направленного вдоль вектора движения молекулы, именно в данный элемент поверхности есть отношение этой площади к полной площади поверхности единичной сферы (равной 4 π):

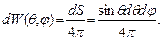(1.1)

Молекулы, вектор направления движения которых попадает в телесный угол dΩ, формируют так называемый подансамбль. Ниже мы часто будем использовать понятие подансамбля для обозначения группы молекул, обладающих близкими значениями некоторой выбранной нами величины или набора величин (в данном случае это углы q и j).

Для краткости можно все же говорить о вероятности иметь направление, характеризуемое углами θ и φ (опуская упоминание об интервалах от θ до θ + dθ и от φ до φ + dφ). Следует, однако, всегда помнить об условности такого словоупотребления.

При аксиальной симметрии от угла φ ничего не зависит. В таком случае вероятность (1.1) можно проинтегрировать по углам φ и получить dW (θ) = . При полном же интегрировании по всей единичной сфере суммарная вероятность иметь все возможные направления равна единице:

Скорости молекул в газе у всех разные. Абсолютная величина скорости меняется от нуля до бесконечности (можно говорить именно о бесконечности, потому что околосветовые скорости для молекул в обычных газах практически недостижимы). Будем говорить о вероятности dW (v) иметь скорость в интервале от v до v + dv. Данная вероятность означает долю частиц, имеющих скорость в этом интервале. Все такие молекулы также формируют подансамбль. Суммарная вероятность иметь всевозможные скорости, как и в предыдущем случае распределения по углам, определяется равным единице интегралом:

(1.2)

Здесь также для краткости можно говорить о вероятности иметь скорость v, то есть, опуская упоминание об интервале от v до v + dv.

Важной характеристикой газа является плотность числа частиц (число молекул в единице объема)

(1.3)

где N – полное число молекул в сосуде, V – объем сосуда.

Среднее значение скорости молекулы есть

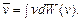(1.4)

Аналогично для среднего значения квадрата скорости

(1.5а)

Можно также говорить о вероятности dW (v _х) иметь скорость v _x вдоль направления х, о вероятности dW (v _у) иметь скорость v_y вдоль направления у, о вероятности dW (v _z) иметь скорость v_z вдоль направления z. Эти проекции скоростей могут быть как положительными, так и отрицательными, и меняются в бесконечных пределах. Для них также справедливы соотношения, аналогичные (1.2), (1.4), (1.5а). Например, среднеквадратичная скорость 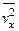дается выражением

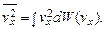(1.5б)

Дата добавления: 2014-01-07