Векторами

Представление синусоидальных величин вращающимися

Величин

Способы представления синусоидальных

Законы Ома и Кирхгофа в комплексной форме.

Способы представления синусоидальных величин.

Лекция 8. Комплексный метод расчета цепей синусоидального тока

Тема 3. Анализ установившегося режима в цепях синусоидального тока

3. Расчет цепей при последовательном и параллельном соединении элементов R, L и C.

Литература: 1.Касаткин А.С. Электротехника: Учеб. для вузов /

А.С.Касаткин, М.В.Немцов. – 8-е изд., испр. – М.:

Издательский центр «Академия», 2003.

2. Теоретические основы электротехники: В 3-х т. Учебник

для вузов. Том 1. – 4-е изд. /К.С.Демирчян, Л.Р.Нейман,

Н.В.Коровкин, В.Л.Чечурин. – СПб.: Питер, 2004.

Известно несколько способов представления синусоидально изменяющихся величин: в виде тригонометрических функций, в виде графиков изменения во времени, в виде вращающихся векторов и, наконец, в виде комплексных чисел.

В первом вопросе лекции были использованы способы представления синусоидально изменяющихся величин в виде тригонометрической (синусоидальной) функции и в виде графика изменений во времени.

Рассмотрим представление синусоидально изменяющихся величин в виде вращающихся векторов и комплексных чисел.

Для представления синусоидально изменяющейся величины

а = А_тsin (w t + y)

с начальной фазой y вращающимся вектором построим радиус-вектор А _m этой величины длиной (в масштабе построения), равной амплитуде А_т, и под углом y к горизонтальной оси (рисунок 1). Это будет его исходное положение в момент начала отсчета времени t = 0.

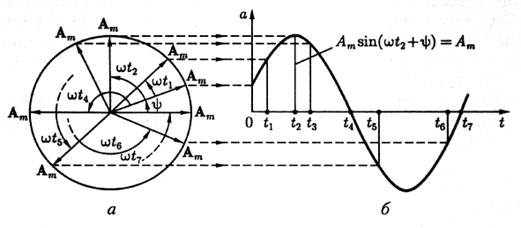
Рисунок 1

Если радиус-вектор вращать с постоянной угловой скоростью w против направления движения часовой стрелки, то его проекция на вертикальную ось будет равна А_тsin (w t + y). По значениям этих величин можно построить график зависимости синусоидальной величины от фазы w t или от времени t. Такое построение приведено для некоторых значений t на рисунке 1, б.

Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты.

Пусть имеем ЭДС е, равную сумме ЭДС е₁ и е₂ одной и той же частоты:

е = е₁ + е₂ = E_1m sin(w t + y₁) + Е_2т sin(w t + y₂) = E_m sin((w t + y).

Изобразим ЭДС е ₁ и е ₂ вращающимися векторами (рисунок 2). Так как проекция на любую ось геометрической суммы двух векторов равна алгебраической сумме их проекций на эту ось, то ЭДС е изображается вращающимся вектором, который равен геометрической сумме векторов, изображающих ЭДС е ₁ и е ₂.

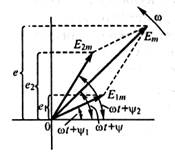
Рисунок 2

При рассмотрении установившихся синусоидальных процессов начальную фазу одной из величин можно выбрать произвольно, например начальную фазу ЭДС или приложенного напряжения. Соответственно произвольно может быть расположен в начальный момент времени вектор, изображающий эту величину. Векторы всех остальных величин при этом будут повернуты по отношению к нему на углы, равные сдвигам фаз.

Совокупность векторов, характеризующих процессы, происходящие в той или иной цепи переменного тока, и построенных с соблюдением правильной ориентации их друг относительно друга, называют векторной диаграммой.

Поскольку на практике обычно интересуются действующими значениями синусоидальных функций, которые в 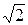меньше их амплитуд, то целесообразно на векторной диаграмме длину векторов выбирать равной в избранном масштабе действующим ЭДС, токам и напряжениям.

Дата добавления: 2014-01-07