Числами

Представление синусоидальных величин комплексными

При выполнении расчетов электрических цепей синусоидального тока удобно пользоваться изображением синусоидальных функций времени комплексными числами. Это позволяет существенно упростить громоздкие записи, которые имеют место при представлении мгновенных значений ЭДС, напряжений и токов.

Как известно из математики, комплексное число может быть представлено с помощью одной из форм записи: показательной, алгебраической и тригонометрической. При показательной форме записи комплексное число представляют с помощью двух величин – модуля А и аргумента y_А в следующем виде

,

где j = 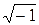- мнимая единица;

е – основание натуральных логарифмов.

При алгебраической и тригонометрической формах записи комплексное число содержит вещественную и мнимую составляющие:

,

.

Существуют следующие связи:

,

,

,

.

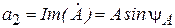Некоторые свойства мнимой единицы, имеющие практический интерес:

, .

Рассмотрим несколько примеров. Пусть имеется синусоидально изменяющийся ток i = I_msin (w t + y _i). Его можно представить в комплексной форме следующим образом

.

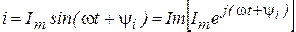Комплексное число

будем рассматривать как символическое изображение действительного синусоидального тока i = I_msin (w t + y _i). При заданной частоте w это комплексное число так же, как и ток i, определяется двумя величинами – амплитудой I_m и начальной фазой y _i. Величина 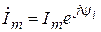получила название комплексная амплитуда.

Для перехода от действительной синусоидальной функции к изображающей ее комплексной величине необходимо модуль последней взять равным амплитуде синусоидальной функции, а аргумент – взять равным аргументу синусоидальной функции. При этом следует иметь в виду, что между этими двумя величинами (действительной и комплексной) нельзя ставить знак равенства. Правильнее будет говорить, что комплексная величина является изображением синусоидальной функции:

.

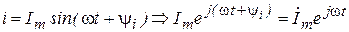При анализе электрических цепей синусоидального тока обычно интересуются действующими значениями ЭДС, напряжений и токов. Комплексные действующие ЭДС, токи и напряжения (или кратко комплексные ЭДС, токи и напряжения) связаны с соответствующими комплексными амплитудами соотношениями:

,

,

.

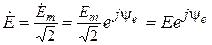Дата добавления: 2014-01-07