Распределение Максвелла

Из предположения о хаотическом характере молекулярного движения следует, что возможно появление молекул с любой скоростью. В главе 1 было введено понятие о вероятностях для молекул dW (v_х), dW (v_у) и dW (v_z) иметь определенную проекцию скорости движения. Обобщением будет введение понятия о вероятности dW (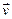) иметь определенное значение вектора скорости 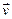, то есть о доле молекул, имеющих скорость в некотором элементе объема d 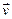пространства скоростей:

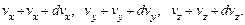(2.1)

Этот элемент объема в пространстве скоростей имеет форму малого прямоугольного параллелепипеда, dW (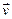) определяет вероятность попадания вектора скорости в этот параллелепипед. В декартовых координатах d 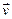= dv_x dv_y dv_z.

Вероятность dW (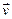) нормирована на единицу:

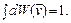(2.2)

Так как вероятность dW (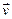) должна быть пропорциональна величине элемента объема d 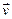, можно говорить о плотности вероятности g (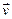), которая равна отношению вероятности dW (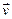) к элементу d :

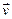dW (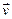) = g (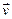) d 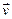. (2.3)

Из принципа равновероятности направлений движения следует, что плотность вероятности не зависит от угловых переменных, указывающих направление вектора скорости, а должна быть лишь функцией его модуля:

g (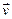) º g (v). (2.4)

Аналогично можно ввести плотности вероятности f (v_х), f (v_y) и f (v_z) того, что молекула имеет компоненты скорости в малых интервалах (2.1):

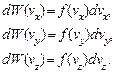(2.5)

В силу хаотичности молекулярного движения, каждая из плотностей вероятностей в (2.5) зависит только от "своей" компоненты скорости и не зависит от других. Кроме того, вид этих функций один и тот же независимо от выбора аргумента v_x, v_y или v_z. То есть, для функциональной зависимости от проекций скоростей используется одно и то же обозначение f.

Введенные плотности вероятности называются еще функциями распределения молекул по скоростям. Отметим, что

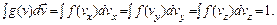
Обладание тем или иным значением одной компоненты скорости никак не зависит от величины других компонент. В соответствии с принципом умножения вероятностей для независимых событий имеем

dW (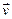) = dW (v_x) dW (v_y) dW (v_z). (2.6)

Здесь под событием подразумевается обнаружение определенного значения одной из компонент скорости. Для плотностей вероятностей f (v_х), f (v_y) и f (v_z) из (2.4) и (2.6) получается соотношение

g (v) = f (v_х)∙ f (v_y)∙ f (v_z). (2.7)

Логарифмирование и последующее дифференцирование (2.7) по v_х дает равенство

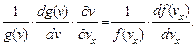(2.8)

Из соотношения между величиной и компонентами скорости 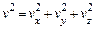получаем, что

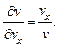(2.9)

Тогда уравнение (2.8) может быть представлено в виде

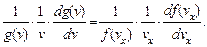(2.10а)

Аналогичные выкладки приводят к аналогичным выражениям и для проекций v _y и v _z.

Равенство (2.10а) утверждает, что функции различных аргументов (v, v_x, v_y, и v_z) совпадают друг с другом во всей области их определения. Такое может быть, только если они все равны одной и той же постоянной. Поэтому перепишем (2.10а) и аналогичные выражения для проекций v_y и v_z в виде

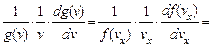
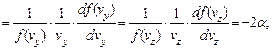(2.10б)

где a – некоторая константа. Множитель -2 перед ней выбран из соображений, которые станут понятны ниже.

Интегрирование представленных в (2.10б) уравнений вида

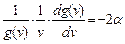
(всего их четыре) дает функции g (v) и f (v_x):

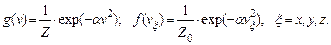(2.11)

Здесь Z и Z ₀ - постоянные интегрирования. Между ними, согласно соотношению (2.7), существует простая связь

Z = Z ₀³. (2.12)

Постоянная Z ₀ может быть найдена, если воспользоваться условием нормировки:

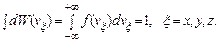(2.13)

Из (2.11) и условия нормировки (2.13) следует, что

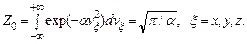(2.14)

Это так называемый интеграл Пуассона. Окончательно

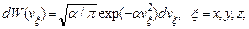(2.15)

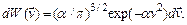(2.16)

Определим, чему равен параметр α. Из распределения (2.15) следует, что

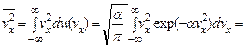
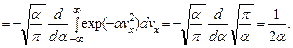(2.17)

Из (1.23) следует, что

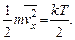
Отсюда

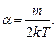(2.18)

Таким образом, предположение о статистической независимости движения в разных направлениях позволило найти распределение молекул по скоростям.

Дата добавления: 2014-01-07