Барометрическая формула и атмосфера Земли

Из опыта известно, что газ в отсутствие внешнего поля равномерно распределен по объему сосуда. Это дает основание считать, что все части объема V сосуда равноправны и вероятность обнаружить молекулу в разных элементах объема dV = dxdydz около точки с координатами x, y, z одинакова. Между тем на практике часто приходится иметь дело с газом, находящимся в потенциальном внешнем поле. Важным примером такого поля является поле тяжести. Пусть ось z системы координат направлена вертикально вверх. Молекула газа в этом поле обладает потенциальной энергией, равной

U = mgz, (3.1)

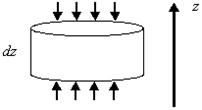
Рис. 3.1.

Будем рассматривать газ в сосуде высотой h, с температурой, одинаковой во всех точках. Выберем в сосуде некоторый горизонтальный слой малой толщины dz (см. рис. 3.1). Вес Р этого слоя компенсируется разностью давлений, действующих снизу и сверху:

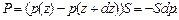(3.2)

С другой стороны, вес газа равен просто весу всех его молекул. Введем плотность газа n (z), которая может зависеть от z. Если слой тонкий, можно пренебречь изменением n (z) в его пределах. Тогда вес определяется формулой:

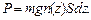(3.3)

Приравнивая (3.2) и (3.3), получим

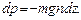(3.4)

Если газ идеальный, то р = nkT, и (3.4) сводится к

dn/n = – mg/kT dz. (3.5)

Интегрируя, получим зависимость плотности от высоты:

n (z) = n (0) exp(– mgz/kT). (3.6)

Полное число молекул N при этом есть

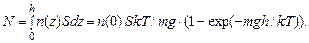(3.7)

Отсюда определяется n (0):

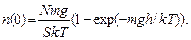(3.8)

Параметр a = mgh/kT характеризует неоднородность распределения газа по высоте. При a >> 1 неоднородность значительна: энергия теплового движения недостаточна, чтобы молекулы могли подняться высоко, и они сосредоточены ближе к дну сосуда. При a << 1 из (3.8) следует, что n (0) = N / Sh, т. е. распределение близко к однородному.

Можно ввести характеристическую длину распределения молекул в поле тяжести (из условия a = 1)

h ₀ = kT/ mg. (3.9)

Для условий земной атмосферы h ₀» 10 км. Сооружаемые емкости имеют значительно меньшие габариты, поэтому неоднородность распределения паров в них не наблюдается. Лишь при подъеме в горы или с помощью авиации обнаруживается влияние поля тяжести на распределение воздуха в атмосфере.

Необходимо подчеркнуть, что формула (3.6) применима только к изотермической атмосфере. Из нее следует барометрическая формула

p (z) = p (0) exp (– mgz / kT). (3.10)

Воздух представляет собой смесь газов, молекулы которых имеют различную массу. В соответствии с формулой (3.6) состав атмосферы должен резко изменяться с высотой. Относительная концентрация легких газов должна увеличиваться с высотой. Измерения состава воздуха на разных высотах не подтвердили этого вывода. Интенсивная конвекция в пределах тропосферы приводит к известному выравниванию состава воздуха по высоте. Общеизвестно также падение температуры с высотой.

Дата добавления: 2014-01-07