Частота столкновений, длина свободного пробега молекул, эффективное сечение

Поставим задачу расчета частоты столкновений молекул в газе. Если газ не очень плотный, то в расчете следует учитывать только двухчастичные столкновения, а столкновениями одновременно более чем двух молекул можно пренебречь.

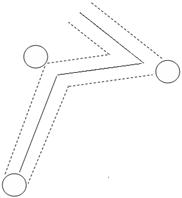
Рис. 5.1.

Выберем некоторую молекулу и будем рассматривать происходящие с ней столкновения. Без ограничения общности можно считать, что относительно выбранной молекулы все остальные молекулы покоятся, а только одна эта молекула движется со скоростью относительного движения 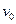. За время t молекула проходит зигзагообразный путь, схематически представленный на рис. 5.1. Так как в газе характерное расстояние между молекулами намного больше их размера (в воздухе при обычных условиях в 10³ раз), искривлением пути в момент столкновения можно пренебречь, и считать, что молекула сталкивается с другими молекулами, находящимися в цилиндре объемом 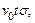где σ - эффективное сечение столкновения. В приближении, в котором молекулы считаются твердыми сферами, 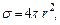где r – радиус сферы (коэффициент 4 появляется из-за суммирования радиусов двух сталкивающихся молекул). Число таких столкновений есть 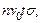где n – концентрация молекул. Усредняя по скоростям, для числа столкновений в единицу времени выделенной молекулы получим

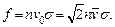
(с учетом (5.2)).

Cредняя длина пробега данной молекулы равна отношению пути, пройденного молекулой, и числа столкновений на этом пути:

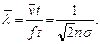(5.4)

Она зависит от плотности газа и эффективного сечения столкновения. В азоте при нормальных условиях . При понижении давления 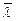возрастает.

В случае молекул примесного газа вместо (5.4) для длины их свободного пробега с учетом (5.3) имеем

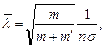
где σ определяется радиусами обеих молекул, σ = p (r ₁ + r ₂)² (плотность n относится к основному газу).

В действительности молекулы взаимодействуют не только при непосредственном соприкосновении, но и при пролете на некотором расстоянии друг от друга. Такой характер взаимодействия учитывается посредством введения эффективного сечения столкновения.

Оценка для азота при нормальных условиях дает ν = 0,8·10¹⁰ с^–1 (n = 2,7·10¹⁹ см ^–3, = 4,5·10⁴ см/с, d = 3,8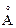). Большое значение f обеспечивает ту быстроту, с которой устанавливается равновесие в газе.

Дата добавления: 2014-01-07