
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операция умножения
|
|
|
|
Умножение в двоичной системе счисления задаются в виде табл. 1.3-3.
Таблица 1.3‑3
| * | ||
Все возможные значения множимого задаются во второй и третьей строках первой колонки. Все возможные значения множителя задаются во второй и третьей колонках первой строки. На пересечении отмеченных значениями операндов строк и колонок располагается результат умножения первого операнда на второй операнд.
При умножении много разрядных операндов, как правило, (особенно в десятичной системе счисления) используется метод, при котором формирование произведения выполняется за счет суммирования частичных произведений, которые формируются посредством умножения множимого на отдельные разряды множителя с учетом веса соответствующего разряда множителя.
Таблица умножения одноразрядных операндов в двоичной системе существенно упрощает задачу формирования частичного произведения:
- частичное произведение для разряда множителя равняется нулю, если этот разряд равен нулю;
- частичное произведение для разряда множителя равняется множимому, взятому с соответствующим весом, если разряд множителя равен единице.
При последовательном способе формирования частичных произведений, последние могут рассчитываться поочередно для отдельных разрядов множителя, начиная с младшего или старшего разряда. При десятичном основании, как правило, формирование частичных произведений осуществляется, начиная с младшего разряда множителя.
Пример1
Найти произведение двоичных чисел 1011 и 1101, начиная формирование частичных произведений со старшего разряда множителя.
Решение
При формировании частичных произведений, начиная со старшего разряда множителя, процесс формирования произведения заданных операндов можно представить следующим образом:
1 0 11
*1 10 1
+ 1 0 1 1
+ 1 0 1 1
+ 0 0 0 0
+ 1 0 1 1
1 0 0 0 1 1 1 1
При реализации умножения рассматриваемым способом требуется использование 2n- разрядного сумматора для подсчета промежуточных и конечного произведения и 2n-разрядного сдвигающего регистра для хранения множителя.
Пример 2
Найти произведение двоичных чисел 1011 и 1101, начиная формирование частичных произведений с младшего разряда множителя и применяя учет сформированных частичных произведений по мере их формирования.
Решение
Реализация данного метода умножения требует использовать 2n-разрядный сумматор для последовательного, от такта к такту, формирования 2n - разрядного произведения и 2n- разрядный регистр для хранения и сдвига влево множимого.
1 0 1 1
* 1 1 0 1
0 0 0 0
+ 1 0 1 1
1 0 1 1
+ 0 0 0 0_
0 1 0 1 1
+ 1 0 11___
1 1 0 1 1 1
+ 1 0 1 1_____
10 0 0 1 1 1 1
Реализация данного метода умножения требует использовать 2n-разрядный сумматор для последовательного, от такта к такту формирования 2n-разрядного произведения и 2n-разрядный регистр для хранения и сдвига влево множимого.
В данном примере для того, чтобы учесть то, что очередной разряд множителя имеет вес, в два раза больший, чем предыдущий разряд, его частичное произведение учитывается со сдвигом на один разряд влево при суммировании с промежуточным результатом. В таком случае говорят, что умножение выполняется со сдвигом множимого.
Однако для того чтобы учесть, что очередное частичное произведение имеет вес, в два раза больший, чем предыдущее, можно при суммировании сдвигать вправо промежуточный результат. В таком случае говорят, что умножение выполнятся со сдвигом промежуточного результата. При использовании такого подхода, умножение чисел 1101 и 1011представляется в виде следующих действий:
| 1 0 1 1 * 1 1 0 1 | множимое множитель | |
| 1р. | 0 0 0 0 + 1 0 1 1 | промежуточный результат (начальное значение). |
| 2р. | 1 0 1 1 0 1 0 1 + 0 0 0 0 | 1 результат сдвига |
| 3р. | 0 1 0 1 0 0 1 0 + 1 0 1 1 | 11 результат сдвига |
| 4р. | 1 1 0 1 01 1 0 + 1 0 1 1 | 111 результат сдвига |
| 1 0 0 0 1 1 0 0 0 | 1111 результат сдвига |
Вторая колонка отражает длину основной разрядной сетки (n = 4).
В первой колонке приведены номера отрабатываемых разрядов множителя, начиная с младшего. Эти номера отмечают строки, в которых учитывается частичное произведение, соответствующее этому разряду множителя. В этой же первой колонке расположены единицы переполнения, возникающие при суммировании промежуточного результата и очередного частичного произведения, сформированного для соответствующего отрабатываемого разряда множителя (в данном случае единица переполнения имеется при отработки четвертого (4р.), самого старшего, разряда множителя).
Вторая колонка представляет собой основную разрядную сетку.
В третей колонке представлены разряды промежуточных и конечного произведений, «вытолкнутых» за пределы основной разрядной сетки в процессе выполнения очередного сдвига промежуточного произведения.
Из приведенного примера видно, что выталкиваемые за пределы разряды промежуточных произведений в дальнейшем не изменяются и их значение не влияет на значение суммы, формируемой в пределах основной разрядной сетки. Поэтому для реализации этого метода умножения требуется n-разрядный сумматор, обеспечивающий суммирования только в пределах основной разрядной сетки.
Аналогично умножению, начиная с младшего разряда множителя, при умножении со старших разрядов можно заменить сдвиг вправо множителя на сдвиг влево промежуточного произведения.
Операция умножения в общем случае дает точный результат - 2п-разрядное произведение, где n - разрядность операндов.
В ЭВМ при выполнении различных операций, в том числе и операции умножения, разрядность операндов и результатов одинаковая. Это означает, что при умножении правильных дробей последние, младшие, n разрядов отбрасываются, а старшие n разрядов округляются с учетом отбрасываемых младших разрядов.
Например, произведение
0.1011*0.1101 = 0.10001111
представляется в n-разрядном варианте как
0.1001.
В этом случае операция умножения считается приближенной.
Иногда в ЭВМ формируется точное произведение; в таких случаях специально оговаривается, что произведение формируется с удвоенной разрядной сеткой.
При операндах, представленных в виде целых чисел, формирование произведения с такой же разрядностью, что и разрядность операндов, в качестве конечного значения произведения также используются n старших разрядов, которые округляются с учетом отбрасываемых младших разрядов. При этом масштаб представления произведения изменяется - он умножается на 2n . Это является одной из причин, по которой в ЭВМ, как правило, используется представление чисел в виде правильных дробей.
Возможные методы реализации операции умножения можно классифицировать по двум признакам:
- начиная с какого разряда (со старшего или младшего) выполняется отработка множителя;
- что сдвигается - множимое или промежуточное произведение.
- Используя эти два классификационных признака, можно выделить четыре метода умножения:
- умножение с младших разрядов множителя со сдвигом множителя; при реализации данного метода требуется 2n- разрядный сумматор, 2n- разрядный регистр промежуточного произведения, 2n - разрядный регистр для хранения и сдвига множимого и n- разрядный регистр для хранения множителя;
- умножение с младших разрядов множителя со сдвигом промежуточного произведения; при реализации данного метода требуется n-разрядный сумматор, 2n-разрядный регистр промежуточного произведения, n-разрядный регистр для хранения множимого и n-разрядный регистр для хранения множителя;
- умножение со старшего разряда множителя со сдвигом множимого; при реализации данного метода требуется 2n-разрядный сумматор, 2n-разрядный регистр промежуточного произведения, 2n-разрядный регистр для хранения и сдвига множимого и n- разрядный регистр для хранения множителя;
- умножение со старшего разряда множителя со сдвигом промежуточного произведения; при реализации данного метода требуется n-разрядный сумматор, 2n-разрядный регистр промежуточного произведения, n-разрядный регистр для хранения множимого и n-разрядный регистр для хранения множителя.
Используя рассмотренные методы умножения, легко показать, что при умножении правильных дробей 0.1011 на 0.1101 будет получено произведение, равное 0.10001111.
Обобщенная структурная схема устройства для реализации операции умножения приведена на рис.1.3-1.
На рисунке приняты следующие обозначения:
- ПК - сигнал разрешения приема кода;
- 1 р. - выход старшего (1-го) разряда множителя (используется при умножении со старших разрядов множителя);
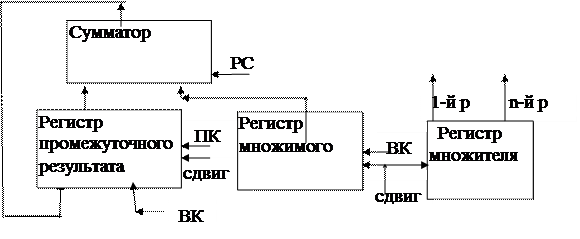 |
Рис. 1.3‑1
- n р. - выход младшего (n-го) разряда регистра (используется при умножении с младших разрядов множителя).
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1500; Нарушение авторских прав?; Мы поможем в написании вашей работы!