Основные понятия алгебры логики. Алгебра логики находит широкое применение при синтезе и анализе схем ЭВМ

Логические основы ЭВМ

Алгебра логики находит широкое применение при синтезе и анализе схем ЭВМ. Это объясняется, с одной стороны, соответствием представления переменных и функций алгебры логики, с другой стороны, двоичным представлением информации и характером работы отдельных компонентов вычислительной техники, которые могут пропускать или не пропускать ток, иметь на выходе высокий или низкий уровень сигнала (напряжения или тока).

Основные понятия алгебры логики:

- логическая переменная - это такая переменная, которая может принимать одно из двух значений: истинно или ложно (да или нет, единица или ноль).

- логическая константа это такая постоянная величина, значением которой может быть: истинно или ложно (да или нет, единица или ноль).

- логическая функция это такая функция, которая может принимать одно из двух значений (истинно или ложно, да или нет, единица или ноль), в зависимости от текущего значений её аргументов, в качестве которых используются логические переменные.

Логическая функция может быть одного (n=1) или нескольких (n >1) аргументов. Значение логической функции определяется комбинацией конкретных значений переменных, от которых она зависит. Комбинация конкретных значений переменных (аргументов функции) называется набором. Проведя аналогию с двоичным кодом, легко убедиться, что количество различных наборов N для «n» переменных определяется как N= 2ⁿ.

Зависимость логической функции от переменных может задаваться по-разному. Это может быть задание функции в виде таблицы истинности, или словесное описание, или задание её в виде логического выражения.

Словесное описание, как правило, может использоваться в случае сравнительно несложной логической функции.

Таблица истинности является универсальным средством задания логической функции. Она включает все наборы для заданного количества переменных, определяющих значение логической функции, с указанием значений, которые принимает функция для каждого набора. В одной таблице истинности может задаваться несколько логических функций, зависящих от одних и тех же переменных. Таблица истинности для нескольких функций y_i трех переменных х₁, х₂, х ₃ может быть задана следующим образом(табл. 2.1-1.):

В приведенной таблице истинности во второй, третей и четвертой колонках, помеченных соответственно х ₁, х₂, х ₃ , приведены все возможные наборы этих переменных. В следующих колонках приводятся значения функций y₁, y₂, y_n для каждого набора.

Таблица 2.1‑1

№ п.п.	х 1	х 1	х 3	y1	y2	y3	.........	yn
								-
								-

Логическая функция, называется «полностью определенная», если для неё заданы значения по всем возможным наборам. Функция, называется «частично определенная», если для некоторых наборов значения функции не заданы. В приведенной таблице истинности функции y₁, y₂, y₃ являются полностью определенными, а функция y_n - частично определенная (знак «-» означает неопределенность значения функции).

Максимальное количество полностью определенных функций от «n» переменных определяется как M = (2²)ⁿ.

Логическим выражением называется комбинация логических переменных и констант, связанных элементарными базовыми логическими функциями (или логическими операциями), которые могут разделяться скобками.

Например, логическую функцию у₁, определенную в вышеприведенной таблице истинности, можно представить в виде логического выражения

где “+”, “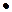”, а также верхнее подчеркивание - знаки базовых логических функций.

Набор элементарных логических операций, с помощью которых можно задать любую, сколь угодно сложную логическую функцию, называется «функционально полная система логических функций». Иногда такую систему называют базисом.

В качестве элементарных логических функций функционально полных систем логических функций используются функции одной или двух логических переменных.

Все возможные функции одной переменой приведены в табл.2.1-2.

Таблица 2.1‑2

№ п.п.	y0	y1	y2	y3

Из таблицы видно, что

- y₀=0 - константа;

- y₁=х - равна значению переменной;

- y₂ - равна значению, обратному значению переменной «х»,

- y₃=1 - константа.

С точки зрения базовых функций интерес представляет только функция y₂, она называется функцией отрицания, читается как «не x» и обозначается как ,

т.е. можно записать

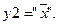
Все возможные функции двух переменных приведены в табл. 2.1-3.

Таблица 2.1‑3

N стр

х1

x2

y0

y1

y2

y3

y4

y5

y6

y7

y8

y9

y10

y11

y12

y13

y14

y15

Информация о функциям двух переменных в приведена в табл. 2.1-4.

Таблица 2.1‑4

yi	название функции	чтение функции	запись в виде булевого выражения
y0	const «0»
y1	конъюнкция	и х1, и х2.	х1* х2;	х1х2; х1Ú х2
y2	запрет по х2	неверно, что, если х1, то х2
y3	f(х1)	функция одной переменной	х1
y4	запрет по х1	неверно, что, если x2, то x1
y5	f(x2)	функция одной переменной	х2
yi	Название функции	Чтение функции	Запись в виде булевого выражения
y6	неравно значности	х1 не равно х2
y7	Дизъюнк ция	или х1, или х2	х1 + х2
y8	Пирса	ни х1, ни х2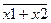
y9	Равнозна чности	х1 равно х2
y10	f(х2)	функция одной переменной
y11	Имплика ция	если x2, то x1.
y12	f(х2)	функция одной переменной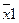
y13	Имплика ция	если x1, то x2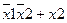
y14	Шеффера	неверно, что и х1, и х2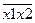
y15	const (=1)

Наиболее распространенной в алгебре логики является функционально полная система логических функций, которая в качестве базовых логических функций использует функцию одной переменной «НЕ» (функция отрицания), и две функции двух переменных - «И» (конъюнкция или логическое умножение) и «ИЛИ» (дизъюнкция или логическое сложение). Эта система получила название система булевых функций или булевый базис. В алгебре логики имеется целый раздел «алгебра Буля»), посвященный этому базису.

В вышеприведенной таблице, описывающей функции от двух переменных, в последней колонке приведены варианты записи этих функций в булевом базисе.

Дата добавления: 2014-01-07