Законы и правила алгебры Буля

Элементы алгебры Буля

В алгебре Буля логические выражения включают логические операции И, ИЛИ, НЕ, которые могут быть использованы в самых различных сочетаниях. При оценки значения такого выражения необходимо решить это выражение для конкретного набора переменных. В алгебре Буля используется следующая приоритетность выполнения операций: сначала рассчитываются значения имеющих место отрицаний и скобок, затем выполняются операция И (логическое умножение); самый низший приоритет имеет операция ИЛИ (логическая сумма).

При работе с булевыми логическим выражениями используются следующие законы и правила.

Переместительный (коммутативный) закон. Закон справедлив как для конъюнкции, так и для дизъюнкции.

х₁ + х₂ + х₃ + х_4.= х₄ + х₃ + х₂+ х₁ - от перемены мест логических слагаемых сумма не меняется.

х₁ х₂ х₃ х_4.= х₄ х₃ х₂ х₁ - от перемены мест логических сомножителей их произведение не меняется.

Этот закон справедлив для любого количества логических операндов.

Сочетательный (ассоциативный) закон. Закон справедлив как для конъюнкции, так и для дизъюнкции.

х₁ + х₂ + х₃ + х_4.= (х₂ + х₃)+ х₁ + х_4.=(х₁ + х₄ )+ (х₂ + х₃) - при логическом сложения отдельные слагаемые можно заменить их суммой.

х₁ х₂ х₃ х_4.= (х₂ х₃₎) х₁х_4.=(х₁ х₄) (х₂ х₃) - при логическом умножении отдельные логические сомножители можно заменить их произведением.

Распределительный (дистрибутивный) закон.

(х₁ + х₂) х_3.= х₁ х₃ + х₂ х₃.

(х₁ + х₂) (х₁ + х₃) = х₁ + х₂ х₃.

Правило де Моргана:

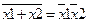-отрицание суммы равно произиедению отрицаний

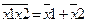- отрицание произведения равно сумме отрицаний

Операция склеивания:

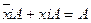- операция склеивания для конъюнкций, где А - переменная или любое логическое выражение.

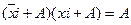- операция склеивания для дизъюнкций.

Если в качестве А используется простая конъюнкция, т.е. конъюнкция, представляющая собой логическое произведение переменных и их отрицаний, то имеет место

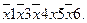
Как видно, в результирующем выражении количество переменных на единицу меньше, чем в склеенных конъюнкциях. Количество переменных в простой конъюнкции называется рангом конъюнкции, т.е. операция склеивания, примененная к простым конъюнкциям, дает результат с рангом, на единицу меньшим ранга исходных конъюнкций.

Операции с отрицаниями:

- двойное отрицание равносильно отсутствию отрицания.

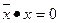
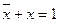
Операции с константами:

х₁ + 1= 1, х₁ + 0= х₁,

х₁ 1= х₁, х₁ 0= 0.

Операции с одинаковыми операндами:

х₁ + х₁ + х₁+ х₁+_... + х₁= х₁ ,

х₁ х₁ х_{1 ....} х₁ = х₁ при любом числе повторений.

Законы и правила алгебры Буля могут быть доказаны путем логического рассуждения, однако такое доказательство применимо только для простейших случаев. Доказать справедливость того или иного правила можно, если с помощью различных преобразований привести правую часть правила к выражению в левой части (или наоборот). Универсальным приемом доказательства является использование таблицы истинности. Это основано на том утверждении, что два выражения (правая и левая часть правила или закона) эквивалентны, если они принимают одинаковые значения на всех наборах логических переменных.

Например, правило двойного отрицания, которое справедливо не только относительно одной переменной, но и любого логического выражения, можно доказать следующим рассуждением: если неверно утверждение, что выражение ложно, то очевидно утверждение, что это выражение истинно.

Доказать справедливость распределительного закона в интерпретации выражением

(х₁ + х₂)(х₁ + х₃)= х₁ + х₂ х₃

можно за счет приведения левой части к выражению правой части, раскрыв скобки:

(х₁ + х₂ *(х₁ + х₃)= х₁ х₂ + х₁ х₁+х₁ х₃.+ х₂ х₃= х₁ х₂ + х₁+х₁ х₃.+ х₂ х₃=

=х₁ (х₂ + 1+ х₃)+ х₂ х₃.

Помня, что логическая сумма с одним слагаемым, равным константе «1», равна «1», можно записать

=х₁+х₂х₃.
Используем таблицу истинности для доказательства правила де Моргана в варианте

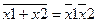- отрицание суммы равно произведению отрицаний.

Составим таблицу истинности для правой и левой частей и составляющих их функций, табл. 2.2-1.

Таблица 2.2‑1

х1	х2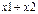

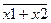
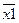
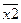
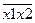
Из таблицы истинности видно, что правая и левая части доказываемого правила принимают одинаковые значения на всех наборах, следовательно они эквивалентны.

Дата добавления: 2014-01-07