Уравнения массоотдачи и массопередачи в локальной форме

Различные модификации уравнений массоотдачи и массопередачи.

Ранее было получено уравнение массопередачи, движущей силой, в которой являлась разница химических потенциалов компонента в ядрах различных фаз. Расчёт химических потенциалов, как известно, задача сложная. Поэтому на практике обычно пользуются уравнениями массотдачи и массопередачи, содержащими в качестве движущей силы разность концентраций компонента.

При использовании интегральной формы уравнений массотдачи и массопередачи большой проблемой является определение поверхности контакта фаз в реальном аппарате, т.к. она может складываться из поверхности струй, капель, пузырей, пены. В этом случае применяют модифицированные уравнения, не содержащие величину межфазной поверхности.

Запишем уравнения массоотдачи для двух фаз G и L. В качестве движущих сил используем разность концентраций.

Предположим, что распределяемый компонент переходит из фазы G в фазу L:

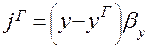(1.15)

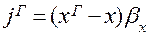(1.16)

где х и у – рабочие концентрации, распределяемого компонента в фазах L и G

соответственно. Используя допущение об отсутствие сопротивления переносу вещества со стороны межфазной поверхности равновесии на границе раздела фаз, запишем:

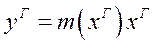(1.17)

Если коэффициент распределения не зависит от состава фазы то

.

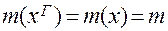Уравнение (1.16) с учетом (1.17) представим в виде:

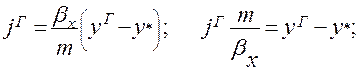а уравнение (1.15) в виде.

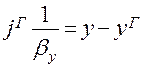Последние соотношения сложим:

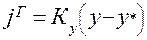(1.18)

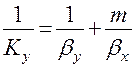или 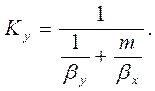(1.19)

Уравнение (1.19) выражает аддитивность фазовых сопротивлений.

Если движущая сила процесса выражается в концентрациях другой фазы L, то уравнение массопередачи примет вид:

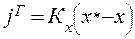(1.20)

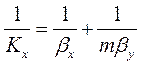
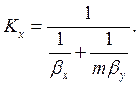(1.19)

Итак, мы получили уравнения массопередачи (1.18) и (1.20), движущими силами в которых являются разности рабочей и равновесной концентрации компонента в одной из фаз. Использование коэффициентов массопередачи Ку или Кх зависит от выбора фазы, через концентрацию, которой записана движущая сила.

Связь между Ку и Кх устанавливается по формулам (1.18) и (1.20) и имеет вид:

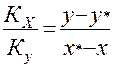(1.22)

В частных случаях, когда m=const получаем:

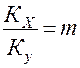
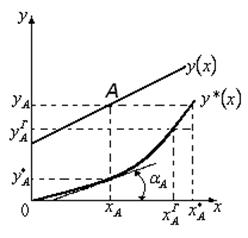
Рис.1.6. Определение коэффициента распределения .

В общем случае зависимость 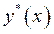представляет собой выпуклую или вогнутую кривую. Однако в рабочем диапазоне изменения параметров эту кривую можно выпрямить, выразив через .Итак имеем:

, , ;

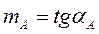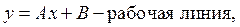
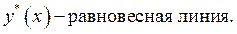
Дата добавления: 2014-01-07