Интегральная форма уравнений массоотдачи и массопередачи

Проинтегрировав уравнения (1.15) и (1.16) по величине межфазной поверхности всего аппарата или его участка можно получить уравнения массоотдачи в интегральной форме:

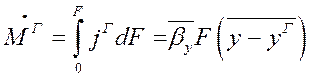
(1.23)

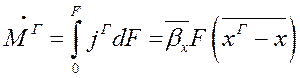
Проведя аналогичную операцию с уравнениями (1.18) и (1.20) получим:

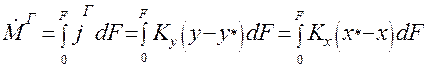(1.24)

Обычно на рассматриваемом участке коэффициенты К_у и К_х могут быть приняты постоянными. Тогда можно записать:

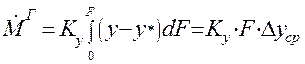(1.25)

(1.26)

По другой фазе:

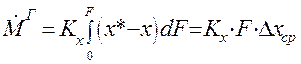(1.27)

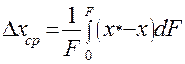(1.28)

Уравнения (1.25) и (1.27) носят название основных уравнений массопередачи. Определим средние движущие силы массопередачи при неизменном расходе по высоте аппарата, пр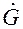и и = const для модели идеального вытеснения (МИВ).

Для элементарного участка dF межфазной поверхности количество распределяемого компонента переносимого из фазы G в фазу L за единицу времени d 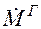можно выразить как:

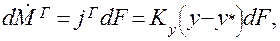(1.29)

Или 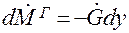(1.30)

Уравнение материального баланса по распределённому компоненту имеет вид:

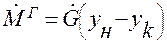(1.31)

Из уравнений (1.29) и (1.30) получим:

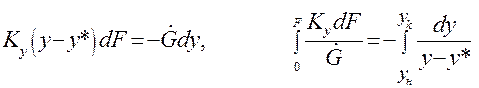(1.32)

Из уравнения (1.31) находим 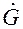и подставляем в (1.32). Тогда получим:

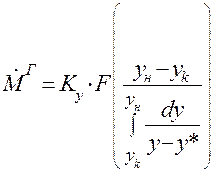(1.33)

Сопоставив уравнения (1.25) и (1.33) находим:

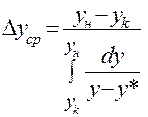(1.34)

Аналогичным путём можно получить:

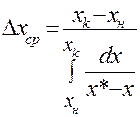(1.35)

В частном случае, если в пределах интегрирования коэффициент распределения m=const (равновесная линия на этом участке прямая, т.е. tgα=const), то 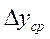имеет вид:

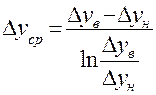(1.36)

Здесь 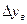и 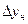движущие силы массопередачи в верхнем и нижнем сечениях аппарата.

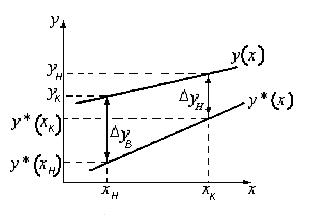
Рис.1.7. Определение средней движущей силы массопередачи.

Аналогичное соотношение справедливо и для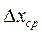

Если линия равновесия обладает существенной кривизной, то аппарат можно разбить на ряд участков и для каждого участка определить свой m.

Структура потока влияет на величину средней движущей силы массопередачи, она максимальна для МИВ, минимальна для МИС.

1.4.3 Объёмные коэффициенты массоотдачи и массопередачи.

В реальном аппарате определить поверхность контакта фаз, зачастую, бывает сложно, т.к. она может складываться из поверхности струй, пузырей, капель и т.д. Необходимо получить уравнения массотдачи и массопередачи, в которые межфазная поверхность не входит.

Введём понятие удельной поверхности контакта фаз 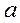, как поверхность контакта, образующаяся в единичном рабочем объёме аппарата:

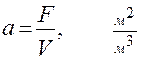(1.37)

Выразив 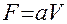, перепишем уравнения массотдачи и массопередачи:

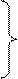
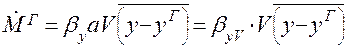(1.38)

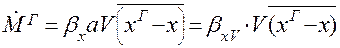
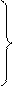
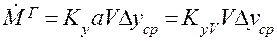(1.39)

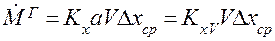
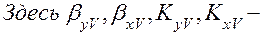объёмные коэффициенты массоотдачи и массопередачи. Определить эти коэффициенты теоретическим путём достаточно сложно. Они, обычно, определяются экспериментально. Связь между обычными и объемными коэффициентами массоотдачи и массопередачи имеет следующий вид:

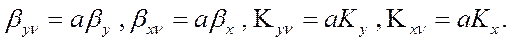
При расчете аппарата со ступенчатым контактом фаз коэффициенты массоотдачи и массопередачи удобнее относить не к объему аппарата, а к площади рабочего сечения контактного устройства 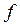, например, площади рабочего сечения тарелки. Вводя удельную поверхность контакта фаз 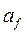(межфазная поверхность, образующаяся на данном контактном устройстве, отнесенная к его рабочему сечению) можно записать уравнение массопередачи следующим образом:

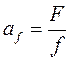(1.40)

(1.41)

Аналогичным образом можно переписать и другие уравнения с использованием коэффициентов массоотдачи и массопередачи, отнесенных к площади рабочего сечения контактного устройства:

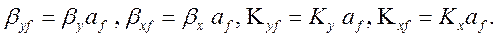
Дата добавления: 2014-01-07