Процессы переноса в ультраразреженном газе

Коэффициенты теплопроводности и вязкости не зависят от плотности газа, так как уменьшение плотности при понижении давления компенсируется увеличением длины свободного пробега молекул. В результате поток тепла между двумя параллельными стенками, имеющими различные фиксированные температуры, не зависит от давления газа. Точно так же, если одна из параллельных пластин движется вдоль самой себя, сила трения, действующая на каждую из пластин, не зависит от давления газа между ними. Однако ясно, что такое невозможно при полном отсутствии газа между стенками (пластинами). Кажущийся парадокс объясняется тем, что применение изложенной выше теории явлений переноса ограничено со стороны низких давлений. Эта теория была развита в предположении о существовании локального термодинамического равновесия, т. е. при выполнении условия где h – характерный линейный размер системы. В разреженном газе длина свободного пробега может так увеличиться, что это условие выполняться уже не будет. Молекулы будут летать, сталкиваясь чаще со стенками сосуда, чем друг с другом. Установление равновесия в таком ультраразреженном газе осуществляется в результате столкновений его молекул со стенками. Если молекулы газа имеют более высокую температуру, то они отдают стенке избыточную энергию и отскакивают (или испаряются при неупругом ударе) уже с температурой стенки. Более холодные молекулы при неупругом столкновении со стенкой приобретают дополнительную энергию. В газе устанавливается равновесие, соответствующее температуре стенок.

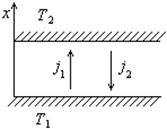
Рис. 6.5

Пусть между двумя параллельными стенками, имеющими температуру , находится такой ультраразреженный газ (рис. 6.5). В стационарных условиях между стенками в каждом из двух противоположных направлений движутся молекулы, обладающие средними энергиями, соответствующие температурам разных стенок, причем их потоки равны:

(6.20)

а плотности в каждом из потоков

Поскольку каждый из потоков (i = 1, 2) формируется при отражении от плоской поверхности практически бесконечных размеров, то распределение соответствующих молекул по направлениям движения можно считать равномерным. Можно поэтому воспользоваться предыдущим результатом (2.27) для суммарного потока молекул на единичную поверхность. Тогда

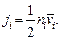. (6.21)

(Здесь множитель ½, а не ¼ как в (2.27), потому что в плотности учитываются только молекулы, летящие в одну сторону).

Из условия равенства потоков нетрудно убедиться, что

(6.22)

Будем считать, что падающие на поверхность 1 молекулы приносят тепло (здесь учитывается, что молекулы в потоке обладают более высокой средней энергией - на величину kT /2 каждая, см. (2.31)), а уносят Для поверхности 2 то же самое, только меняются индексы. Тогда создаваемый от поверхности 1 к поверхности 2 поток энергии равен

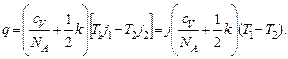(6.23)

С учетом (6.22):

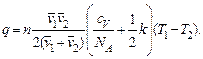(6.24)

Таким образом, поток тепла в ультраразреженном газе линейным образом зависит от плотности газа.

Аналогично может быть рассмотрено молекулярное течение между двумя параллельными пластинами, движущихся вдоль самих себя в одном направлении. Для силы трения тогда получается выражение

(6.25)

где S – площадь пластины. Если температуры пластин одинаковы, то эта формула упрощается:

(6.26)

Физический смысл результата прозрачен: на единицу поверхности в единицу времени ударяется молекул, каждая из них передает верхней пластине импульс

Дата добавления: 2014-01-07