Подвижность частиц. Связь между коэффициентами подвижности и диффузии

Пусть на частицы (они могут быть как макроскопическими, так и молекулярных размеров) действует постоянная сила (например, сила тяжести для макроскопических частиц, для ионов в газе это сила со стороны внешнего электрического поля и т. д.). Частица также испытывает столкновения с окружающими молекулами. В результате частица участвует в хаотическом тепловом движении и одновременно под действием силы приобретает скорость регулярного движения в сторону действия этой силы. После усреднения по временам пробега получим

(6.16)

где коэффициент пропорциональности 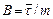называют подвижностью частицы.

Так как то

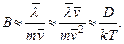(6.17)

Эта формула, устанавливающая связь между коэффициентами диффузии и подвижности, хотя и получена приближенно, на самом деле является точной. Докажем это. В поле силы частица обладает потенциальной энергией 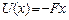(ось x направлена в сторону действующей силы). Если состояние стационарное и температура постоянна, то концентрация частиц меняется в пространстве в соответствии с формулой Больцмана:

(6.18)

Из-за действия силы возникает поток, величина которого ей пропорциональна, как это следует из (6.16). Также эта величина пропорциональна плотности, т. е.

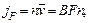
С другой стороны, из-за градиента концентрации имеется направленный противоположно диффузионный поток

В состоянии равновесия суммарный поток частиц равен нулю:

.

С использованием распределения Больцмана (6.18) из последнего равенства получается соотношение, связывающее коэффициент диффузии и подвижность частиц:

. (6.19)

Оно было установлено Эйнштейном и носит его имя.

Дата добавления: 2014-01-07