Некогерентного накопления

НЕКОГЕРЕНТНОЕ НАКОПЛЕНИЕ СИГНАЛА. АНАЛИЗ КАЧЕСТВА

а) Структурная схема обнаружителя

Оптимальное обнаружение некогерентных сигналов предусматривает вычисление модульных значений корреляционных интегралов ½z_i½ (внутриимпульсное накопление) и суммирование в общем случае нелинейных функций этих модульных значений (межпериодное некогерентное накопление). Вид функции определяет вид детектирования (линейный или квадратичный), а операцию суммирования после детектирования называют некогерентным накоплением.

Введем амплитудные множители S_i, которые характеризуют форму пачки. Примем для наибольшего импульса пачки S_i=S=1.

Тогда можно записать

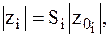
где величины z_0i соответствуют однотипнo получаемым импульсам x₀(t) (т.е. S=1).

Значения ½z_0i½ могут быть сняты с выхода единственного канала приема последовательно во времени. Достаточно, чтобы этот канал содержал схему когерентной обработки ожидаемого сигнала x_0i(t) (коррелятор или фильтр) и линейный детектор.

Для получения квадратов z_0i² линейный детектор следует заменить квадратичным.

После детектирования необходимо осуществить весовое суммирование, например, с использованием линии задержки с отводами. Структурная схема типового обнаружителя некогерентной пачки сигналов представлена на рис. 2.

Весовые коэффициенты k_i учитывают как влияние огибающей пачки S_i, так и весовые коэффициенты в достаточных статистиках (ln l).

В случае слабой нефлюктуирующей пачки, когда оптимален квадратичный детектор, последетекторное суммирование импульсов производится с весовыми коэффициентами k_i=S_i², т.к.

В случае нефлюктуирующей пачки импульсов большой амплитуды оптимален линейный детектор и последетекторное суммирование производится с весовыми коэффициентами k_i=S_i поскольку

Наконец, в случае флюктуирующей пачки оптимален квадратичный детектор и последетекторное суммирование производится с весовыми коэффициентами , где - отношение сигнал/помеха для импульса с весовым множителем единица, средняя энергия которого равна Э₀. В этом случае

где .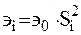

В радиолокационных станциях с визуальной индикацией некогерентное накопление осуществляется на экране индикатора за счет явления послесвечения. Если, например, отметка яркостная, то области свечения, возбужденные отдельными импульсами, при обзоре сливаются в единую дужку. Такое накопление по своему эффекту приближается к квадратичному, хотя, естественно, отличается от оптимального.

При автоматизированном съеме данных некогерентное накопление можно реализовать с помощью линий задержки, потенциалоскопов и т.п. Отсутствие какого-либо последетекторного накопления при автоматизированном съеме может значительно ухудшить условия обнаружения, даже по сравнению с визуальным съемом. Поэтому отказ от некогерентного суммирования недопустим.

Таким образом, устройство оптимального обнаружения некогерентной пачки когерентных сигналов включает блок оптимальной обработки когерентных составляющих и блок последующего некогерентного накопления сигналов пачки.

б). Качественные показатели обнаружения некогерентных сигналов

Напряжение на выходе идеального квадратичного сумматора можно представить в виде

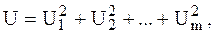
для линейного сумматора

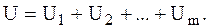
Здесь U₁, U₂,...,U_m - амплитуда первого, второго и М-го импульсов соответственно. При отсутствии сигнала эти амплитуды - независимые случайные величины, подчиняющиеся закону Релея. При наличии сигнала распределение каждой из амплитуд меняется. Зная законы распределения амплитуд, можно найти плотности вероятности P_сп(U) и P_п(U) суммарной величины U при наличии и отсутствии полезного сигнала. Интегрируя эти плотности вероятности в пределах от порогового значения U₀ до ¥, можно перейти к условным вероятностям правильного обнаружения D и ложной тревоги F и оценить выигрыш некогерентного суммирования импульсов по сравнению с приемом одного из них. Вычисление вероятностей D и F для некогерентных сигналов - весьма трудоемкая задача. Поэтому ограничимся анализом конечных результатов.

Кривые для оценки выигрыша некогерентного суммирования нефлюктуирующей пачки с прямоугольной огибающей приведены на рис. 3.

	Рис. 3.

Эти кривые построены при фиксированных значениях D=0,5 и F=10^-10 (сплошная - для линейного, пунктирная - для квадратичного суммирования). По оси ординат отложено число суммируемых импульсов М, по оси абсцисс - необходимое превышение энергии одного импульса Э_и над спектральной плотностью шума на входе устройства оптимальной обработки. Величина превышения 13,5 дБ при М=1 соответствует точке F=10^-10, D=0,5 кривой обнаружения одиночного сигнала со случайной начальной фазой. Небольшое расхождение сплошной и пунктирной кривых на рис.3а показывает, что при малом уровне ложной тревоги и большой вероятности правильного обнаружения переход от квадратичного суммирования к линейному практически не меняет порогового сигнала. Оба рассмотренных вида неоптимальной обработки хорошо аппроксимируют оптимальную обработку (где С - постоянная, зависящая от уровня помехи), соответствующую линейному суммированию при больших и квадратичному при малых уровнях сигнала. Интегрирование большого числа импульсов понижает пороговый уровень энергии каждого импульса в пачке. При переходе от одного импульса к 10 пороговый уровень снижается на 8 дБ, при переходе к 100 - на 15,5 дБ, а при переходе к 10000 импульсам в пачке - на 25,5 дБ.

На рис. 3б нанесены кривые для оценки выигрыша от некогерентного суммирования (сплошная линия) и когерентного (пунктир) для вероятностей D=0,9 и F=10^-7. Как видно из сопоставления кривых на рис. 3 требования D=0,5, F=10^-10 и D=0,9, F=10^-7 при некогерентном суммировании практически эквивалентны, т.е. имеет место почти одинаковый выигрыш в пороговой энергии импульса. Пользуясь одной из них, можно ориентировочно построить аналогичную кривую для произвольных значений D, F путем смещения ее вправо или влево относительно точки с абсциссой 13,5 дБ и ординатой М=1. Смещение должно соответствовать изменению пороговой энергии одиночного импульса в децибелах при переходе к новым значениям D и F. Аналогично можно оценить влияние дружных флюктуаций пачки при произвольном М, взяв для заданных D, F поправку на эти флюктуации из кривых обнаружения.

Представляет значительный интерес сравнение некогерентного суммирования с когерентным. Легко убедиться, что когерентное суммирование даетбольший выигрыш, так как наилучшим образом использует энергию всей пачки. Поэтому при переходе, например, от одного импульса к 10 пороговая энергия каждого импульса уменьшается в 10 раз, т.е. на 10 дБ (а не на 8 дБ, как при некогерентном суммировании), при переходе к 100 импульсам - в 100 раз, т.е. на 20 дБ (а не на 15,5) и т.д. На рис. 4 построен график потерь в децибелах некогерентного суммирования (некогерентного интегрирования) по отношению к когерентному для D=0,9, F=10^-7.

При небольшом числе импульсов потери сравнительно невелики, но с увеличением числа импульсов в пачке, когда при заданных D, F и энергии пачки Э уменьшается энергия каждого импульса, они становятся значительными. Например, для М=10 потери равны всего 2 дБ, а при М=1000 потери составляют уже около 10 дБ. Тем не менее, некогерентное суммирование дает большой эффект и когда когерентное суммирование невозможно, нужно использовать некогерентное.

Таким образом, некогерентное накопление уступает по качеству когерентному, однако во многих случаях оно является либо единственно возможным, либо наиболее просто реализуемым.

Дата добавления: 2014-01-07