Формула Стокса

В двух изложенных выше задачах удается получить точное решение. В более сложных ситуациях возникают, однако, большие математические трудности. Но есть довольно простой физический подход, который основан лишь на соображениях размерности. Он заключается в том, что часто ответ можно просто «угадать», исходя из размерности физических величин, от которых этот ответ может зависеть. Разумеется, в таком подходе решение определяется с точностью до неизвестного числового коэффициента.

Рассмотрим движение шара в вязкой жидкости. Шар движется с некоторой скоростью u. Попробуем определить силу сопротивления F, испытываемую этим шаром. (задача обратная задаче обтекания неподвижного шара потоком жидкости со скоростью u, обе задачи эквивалентны). В задаче имеется всего четыре параметра: радиус шара a (размерность см), плотность жидкости ρ (г см^–3), вязкость η (г сек^–1×см^–1), скорость движения шара u (см сек^–1). Попробуем «угадать», какой должна быть сила F (г×см сек^–2). Подсказкой здесь является выражение (7.5), из которого следует, что эта сила пропорциональна скорости и вязкости. Дальше будем действовать, исходя лишь из соображений размерности. Чтобы напряжение силы в (7.5) превратить в саму силу, надо это напряжение умножить на величину размерности площади. В результате получится, что сила пропорциональна еще и величине размерности длины. Тогда для искомой силы можно написать:

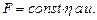(7.11)

Оказывается, что формула вида (7.11) представляет собой единственную комбинацию указанных размерностей. (Причем плотность жидкости в нее не входит).

Коэффициент пропорциональности в (7.11) требует сложных вычислений. Оказалось, что 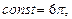то есть

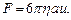(7.12)

Эта формула называется формулой Стокса.

Если помещенный в жидкость шар начинает в ней падать под влиянием действующей на него силы тяжести P (с учетом частичной потери веса в жидкости), то увеличение скорости в ходе падения будет происходить до тех пор, пока сила сопротивления (7.12) не скомпенсирует силу P. Тогда скорость падения станет постоянной; из условия P = F она находится как

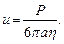(7.13)

Скорость падения u согласно (7.13) должна уменьшаться с ростом вязкости и с уменьшением размера а (вес P пропорционален а ³).

Отметим, что появившийся в (7.13) коэффициент пропорциональности между силой и скоростью соответствует введенной в (6.16) подвижности частицы:

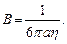(7.14)

Измерение скорости падение шарика можно использовать для определения вязкости жидкости. Вязкость можно определить и с помощью формулы Пуазейля (7.10), измеряя скорость вытекания жидкости из трубки под действием внешнего давления.

Дата добавления: 2014-01-07