Формула Пуазейля

Рассмотрим течение жидкости по цилиндрической трубе радиуса R и длины L. На концах трубы поддерживаются различные давления p ₁ и p ₂, за счет перепада которых 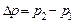и происходит движение жидкости. Скорость u (r) течения жидкости направлена везде вдоль оси трубы и зависит от расстояния r от оси. Для напряжения силы трения справедливо выражение

(7.6)

Рассмотрим объем жидкости, ограниченный проведенной внутри трубы коаксиальной с ней цилиндрической поверхностью некоторого радиуса r (см. рис. 7.2).

Рис. 7.2

Сила трения, действующая на рассматриваемый объем жидкости, определяется умножением напряжения τ и площади поверхности 2 πrL:

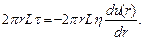(7.7)

Данная сила трения, действующая на рассматриваемый объем жидкости, компенсируется силой, возникающей из-за перепада давлений, действующих у оснований цилиндра, которая равна πr ²∆ p. Приравнивая эти силы, получим уравнение

откуда

Постоянная в этом решении определяется из условия равенства нулю скорости на поверхности трубы, т. е. при r=R.. Отсюда:

(7.8)

Как видно из (7.8), скорость меняется по квадратичному закону от нуля на стенке до максимального значения 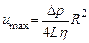на оси трубы (говорят о параболическом профиле скоростей), см. рис. 7.3.

рис. 7.3

Отметим, что скорость u (r) согласно (7.8) пропорциональна градиенту скорости и обратно пропорциональна вязкости η.

Определим объем жидкости, вытекающей из трубы в единицу времени. Выделим два коаксиальных цилиндра с радиусами r и r + dr (см. рис. 7.2). Можно считать, что жидкость между стенками цилиндров движется с одной и той же скоростью 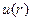. Тогда объем этой жидкости, вытекающий за единицу времени, есть

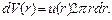
Подставляя сюда (7.8), получим:

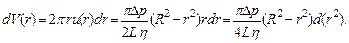
После интегрирования получим:

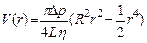(7.9)

(постоянная интегрирования равна нулю, так как должно быть V (0) = 0). Полный объем жидкости, вытекающей из трубы за одну секунду, есть значение (7.9) при :

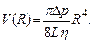(7.10)

Эта формула называется формулой Пуазейля. Cогласно этой формуле, объем жидкости, вытекающей из трубы, пропорционален разности давлений, четвертой степени радиуса трубы и обратно пропорционален вязкости.

Дата добавления: 2014-01-07