Лекция № 6. Плоскопараллельное движение твердого тела

Цель: Изучить законы плоскопараллельного движения твердого тела.

Воспитательная цель: Показать применение математических методов при решении технических задач

Плоскопараллельным движением называется такое движение, при котором все точки тела перемещаются в плоскостях параллельно какой-то одной плос­кости, называемой основной. Пример такого движения: движение колеса автомобиля на прямом участке пути, движение шатуна кривошипно-шатунного механизма.

Плоскопараллельное движение изучается двумя методами:

1) методом разложения плоскопараллельного движения на поступатель­ное и вращательное;

2) методом мгновенных скоростей.

В основе первого метода лежит теорема: всякое плоскопараллельное движение может быть получено с помощью одного поступательного и одно­го вращательного движения (рис. 1.48).

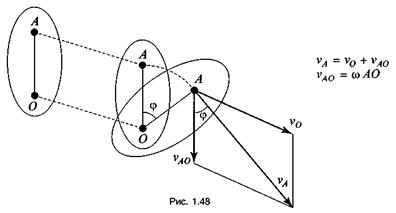
Плоскопараллельное движение тела может осуществляться путем одно­временно происходящих вращательных и поступательных движений.

Поступательное движение тела можно считать переносным, а вращатель­ное — относительным. Тогда вектор абсолютной скорости какой-то точки А будет равен скорости поступательного движения какой-то другой точки О плюс скорость вращательного движения точки А относительно точки О (см. рис. 1.48):

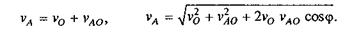
Точка, вокруг которой происходит относительное вращательное движе­ние, называется полюсом вращения.

Таким образом, скорость любой точки тела при плоскопараллельном дви­жении в данный момент времени равна сумме скорости полюса вращения и вращательной скорости данной точки относительно полюса:

В основе второго метода лежит понятие мгновенного центра скорос­тей (МЦС).

Мгновенный центр скоростей — это точка плоской фигуры, скорость ко­торой в данный момент времени равна нулю.

Всегда можно на фигуре найти такую точку. Например, возьмем скорость какой-то точки А, которую примем за полюс вращения. Отложим отрезок АР, перпендикулярный v_A, где АР = v_A / ω, тогда скорость точки Р равна 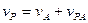, причем (рис. 1.49). Таким образом,

Мгновенный центр скоростей всегда лежит на пря­мой, проведенной из какой-либо точки фигуры пер­пендикулярно направлению скорости этой точки.

Скорость любой точки фигуры прямо пропорцио­нальна ее расстоянию до МЦС:

Способы нахождения МЦС:

1. Известны угловая скорость и скорость какой-то точки.

В этом случае МЦС точки Р находится на перпен­дикуляре, восстановленном из точки А к вектору ско­рости на расстоянии АР = v_A / ω (см. рис. 1.49):

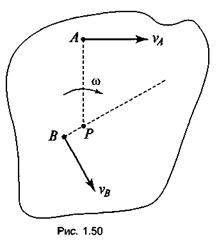
2. Известны направления скоростей двух точек v_A и v_B.

В этом случае МЦС лежит на пересечении перпендикуляров, восстанов­ленных из точек А и В к направлениям их скоростей (рис. 1.50).

3. Известно, что векторы скорости двух точек v_A и v_B параллельны друг дру­гу, направлены в одну сторону перпендикулярно отрезку АВ и не равны повеличине.

В этом случае МЦС находится в точке пересечения прямой, соединяющей начала векторов v_A и v_B, с прямой, соединяющей их концы (рис. 1.51).

4. Известно, что векторы скорости двух точек v_A и v_B параллельны друг другу, но направлены в противоположные стороны.

В этом случае МЦС находится на пересечении прямых, соединяющих начала и концы векторов скорости (рис. 1.52).

5. Известно, что плоская фигура без скольжения катится по неподвижной прямой.

В этом случае МЦС находится в точке соприкосновения фигуры с пря­мой (рис.1.53).

Дата добавления: 2014-01-07